Question 323171: A group of twenty-five coins, whose total value is $2.75, is composed of nickels, dimes, and quarters. If the nickels were dimes, the dimes were quarters, and the quarters were nickels, the total would be $3.75. How many quarters are there in the collection?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A group of twenty-five coins, whose total value is $2.75, is composed of
nickels, dimes, and quarters. If the nickels were dimes, the dimes were
quarters, and the quarters were nickels, the total would be $3.75.
How many quarters are there in the collection?
:
Write an equation for each statement:
A group of twenty-five coins,
n + d + q = 25
:
whose total value is $2.75,
we can use cents here
5n + 10d + 25q = 275
:
If the nickels were dimes, the dimes were quarters, and the quarters were nickels, the total would be $3.75.
10n + 25d + 5q = 375
:
Multiply the 1st equation by 5, subtract from 2nd equation
5n + 10d + 25q = 275
5n + 5d + 5q = 125
---------------------subtraction eliminates n
5d + 20q = 150
:
multiply the 1st equation by 10, subtract from the 3rd equation
10n + 25d + 5q = 375
10n + 10d + 10q =250
-------------------------- subtraction eliminates n
15d - 5q = 125
:
Multiply 5d + 20q = 150 by 3, subtract the above equation
15d + 60q =450
15d - 5q = 125
------------------- subtraction eliminates d, find q
65q = 325
q = 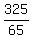
q = 5 quarters
:
:
To check solution, find d
5d + 20q = 150
replace q with 5
5d + 20(5) = 150
5d = 150 - 100
d = 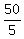
d = 10
then
n = 10 also (total coins is 25)
:
Check in the 2nd equation
5(10) + 10(10) + 25(5) =
50 + 100 + 125 = 275
|
|
|