Question 321896: Sir/Madam,
How are you today,I am requesting you kindly to help me with 4 problems,I need to give positive values of the angle between 0degrees and 360degrees ,that will satisfy each and give approximate value to the nearest minutes.So far this is what i have tried: e.[sin(theta)=sqrt3/2] =[sin60dgrs=sqrt3/2]therefore,60dgrs and 120dgrs are the required value of(theta).f. (sin 2x=cos 2x)= (22 30',112 30',202 30,292 30')letter f,I have shown only the answer b'se of time. These are the 4 problems i need help with:
a.[sin(2x-10degrees)=1/2]; b.[cos 2x-sin^2(x/2+3/4)=0]; c.[sin^2(theta)=cos^(theta)+1/2]; d.[tan(x+15degrees)=3 tan x] P'se show work.Thanks much!
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! a. sin(2x-10degrees)=1/2
(2x - 10) = 30, 150, 390, 510 degs
2x = 40, 160, 400, 520º
x = 20, 80, 200, 260º
--------------------------
b. cos 2x-sin^2(x/2+3/4)=0
cos(2x) = 1 - 2sin^2(x)
1-sin^2(x) - sin^2(x/2 + 3/4) = 0
sin^2(x) + sin^2(x/2 + 3/4) = 1
Is there a typo?
-------------------
c. sin^2(theta)=cos^(theta)+1/2
Is that cos^2 ?? If so,
cos^2(t) - sin^2(t) = -1/2
cos(2t) = -1/2
2t = 120, 240, 480, 600º
theta = 60, 120, 240, 300º
----------------------------
d tan(x+15degrees)=3 tan x
(tan(x) + tan(15))/(1 - tan(x)*tan(15)) = 3tan(x)
tan(x) + tan(15) = 3tan(x) - 3tan^2(x)*tan(15)
3tan(15)*tan^2(x) - 2tan(x) + tan(15) = 0
tan(15) = tan(30/2) = sin(30)/(1+cos(30)) = (1/2)/(1 + sqrt(3)/2)
tan(15º) = 1/(2 + sqrt(3)) = 2 - sqrt(3)
-----------------------------------------
3tan(15)*tan^2(x) - 2tan(x) + tan(15) = 0 is a quadratic in tan(x).
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=3.13843876330611 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 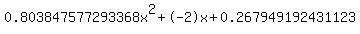 can be factored: can be factored:

Again, the answer is: 2.34594470271034, 0.142089169002246.
Here's your graph:
 |
=====================================
tan(x) = 0.142089169
x =~ 8.132 degs
-----------------
tan(x) = 2.3459447027
x =~ 66.913 degs
|
|
|