Question 320851: From a pile of 100 pennies, 100 nickles , and 100 dimes . select 21 coins which have a total of exactly $1.00 . how many of each of the three types should be selected?
Found 2 solutions by Edwin McCravy, JBarnum:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Eliminate n by multiplying the first equation through by -5
Eliminate n by multiplying the first equation through by -5
 Adding these term by term:
Adding these term by term:
 The smallest absolute value of a coefficient is 4,
so write all integers in terms of their nearest multiple
of 4
The smallest absolute value of a coefficient is 4,
so write all integers in terms of their nearest multiple
of 4

 Divide through by 4
Divide through by 4
 Isolate fractional terms:
Isolate fractional terms:
 The right side is an integer, so let that integer be A,
set both sides equal to integer A:
The right side is an integer, so let that integer be A,
set both sides equal to integer A:
 Clear the first equation of fractions:
Clear the first equation of fractions:
 Solve the first equation for d
Solve the first equation for d
 Substitute that for d in
Substitute that for d in 




 Subsitutute
Subsitutute  and and  in in 



 So now we have the numbers of coins in terms of integer A
So now we have the numbers of coins in terms of integer A
 10 dimes makes a dollar so there can't be as many as 10 dimes, since
we have to have 21 coins, so
10 dimes makes a dollar so there can't be as many as 10 dimes, since
we have to have 21 coins, so

 Add 1 to all three sides:
Add 1 to all three sides:
 Divide all three sides by 4
Divide all three sides by 4

 Since A is an integer then A is either 1 or 2, for
they are the only integers between
Since A is an integer then A is either 1 or 2, for
they are the only integers between  and and 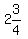 So there will be two solutions,
If A = 1, then
So there will be two solutions,
If A = 1, then
 So that's one solution: 5 pennies, 13 nickels and 3 dimes.
If A = 2, then
So that's one solution: 5 pennies, 13 nickels and 3 dimes.
If A = 2, then
 So that's the other solution: 10 pennies, 4 nickels and 7 dimes.
Edwin
So that's the other solution: 10 pennies, 4 nickels and 7 dimes.
Edwin
Answer by JBarnum(2146)   (Show Source): (Show Source):
|
|
|