SOLUTION: From a pile of 100 pennies, 100 nickles and 100 dimes, select 21 coins which have a total of $1.00. how many of each coin should be selected.

Algebra ->  Customizable Word Problem Solvers  -> Coins -> SOLUTION: From a pile of 100 pennies, 100 nickles and 100 dimes, select 21 coins which have a total of $1.00. how many of each coin should be selected.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 320840: From a pile of 100 pennies, 100 nickles and 100 dimes, select 21 coins which have a total of $1.00. how many of each coin should be selected.
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Sorry. You can't get there from here. The dimes have the largest value, so the largest amount that can be represented by 21 coins is 21 dimes. 21 dimes are worth $2.10, no where close to $100.


John

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

It's obvious you meant $1.00 but left off the decimal. I changed it for you.

system%28p%2Bn%2Bd=21%2Cp%2B5n%2B10d=100%29

Eliminate n by multiplying the first equation through by -5

system%28-5p-5n-5d=-105%2Cp%2B5n%2B10d=100%29

Adding these term by term:

-4p%2B5d=-5

The smallest absolute value of a coefficient is 4,
so write all integers in terms of their nearest multiple
of 4

-4p%2B%284%2B1%29d=-%284%2B1%29
-4p%2B4d%2Bd=-4-1

Divide through by 4

-p%2Bd%2Bd%2F4=-1-1%2F4

Isolate fractional terms:

d%2F4%2B1%2F4=p-d-1

The right side is an integer, so let that integer be A, 
set both sides equal to integer A:

system%28d%2F4%2B1%2F4=A%2Cp-d-1=A%29

Clear the first equation of fractions:

system%28d%2B1=4A%2Cp-d-1=A%29

Solve the first equation for d

d=4A-1

Substitute that for d in p-d-1=A

p-d-1=A
p-%284A-1%29-1=A
p-4A%2B1-1=A
p-4A=A
p=5A

Subsitutute p=5A and d=4A-1 in p%2Bn%2Bd=21

p%2Bn%2Bd=21
5A%2Bn%2B4A-1=21
9A%2Bn-1=21
n=22-9A

So now we have the numbers of coins in terms of integer A

system%28p=5A%2C+n=22-9A%2C+d=4A-1%29

10 dimes makes a dollar so there can't be as many as 10 dimes, since
we have to have 21 coins, so

0%3C=d%3C10

0%3C=4A-1%3C10

Add 1 to all three sides:

1%3C=4A%3C11

Divide all three sides by 4

1%2F4%3C=A%3C11%2F4
1%2F4%3C=A%3C2%263%2F4

Since A is an integer then A is either 1 or 2, for
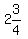they are the only integers between 1%2F4 and 2%263%2F4
So there will be two solutions,

If A = 1, then 

system%28p=5A=5%281%29=5%2C+n=22-9A=22-9%281%29=22-9=13%2C+d=4A-1=4%281%29-1=4-1=3%29

So that's one solution 5 pennies, 13 nickels and 3 dimes.

If A = 2, then 

system%28p=5A=5%282%29=10%2C+n=22-9A=22-9%282%29=22-18=4%2C+d=4A-1=4%282%29-1=8-1=7%29

So that's the other solution 10 pennies, 4 nickels and 7 dimes.

Edwin