Question 320331: Ann is driving a motorboat across a river that 2 km wide. The boat has a speed of 20 km/h in still water, and the current in the river is flowing at 5km/h. Ann heads out from one bank of the river for a dock directly across from her on the opposite bank. She drives the in a direction perpendicular to the current. How far downstream from the dock will Ann land? And how long to cross the river?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The river is 2 km wide.
The boat is traveling at 20 km/h in a straight path directly across the river.
The stream is traveling at 5 km/h in a straight path directly down the river which is perpendicular to the direction the boat is traveling.
Since the river is traveling in a perpendicular direction to the direction the boat it traveling, it has no impact on the lateral speed of the boat. That lateral speed is still 20 km/h.
Since the river is 2 km wide, then the boat will take 2/20 hours to cross which equates to .1 hours which equates to 6 minutes.
In the same .1 of an hour, the boat will also be pushed downstream by the current.
Since the current is traveling at 5 km/h, the boat will be pushed 5 * .1 = .5 km downstream.
This is because Rate * Time = Distance.
Rate is the speed of the current and Time is the time it took the boat to reach the other side of the river, so the distance is 5 * .1 = .5 as shown above.
Ann will land .5 km downstream from the dock and it will take .1 of an hour or 6 minutes to make the crossing.
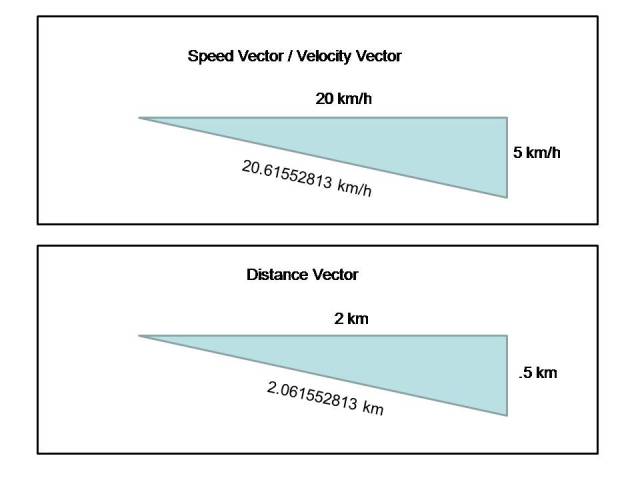
What you are doing here is adding vectors.
There is a speed vector and a distance vector involved.
First the speed vector.
You break the vectors down into x components and y components.
If you let the direction the boat is traveling equal to the x component, then the direction the current is traveling is equal to the y component.
First we look at the speed vector (velocity).
The x component of the speed of the boat is 20 km/h and the y component is 0.
The x component of the speed of the current is 0 km/h and the y component is 5.
Add these vectors together and you get a combined x component of 20 and a y component of 5.
This forms a right triangle where the hypotenuse is the actual speed of the boat taking into consideration the speed of the boat and the speed of the current.
This becomes the square root of (20^2 + 5^2) = the square root of (425) which becomes 20.61552813.
The actual speed of the boat taking into consideration the speed of the current plus the speed of the boaqt is 20.61552813 km /h.
Now the distance vectors come into play.
The x component of the distance vectors is 2 km which is the width of the river.
Since we know the x component of the speed and the x component of the distance, we can calculate how long it takes the boat to cross the river.
That time is .1 hours which equates to 6 minutes.
At the same time, the current is pushing the boat downstream at 5 km / h.
.1 * 5 = .5 km.
We now have 2 distances which are the x component of the distance vector and the y component of the distance vector.
We can calculate the distance the boat is traveling by taking the speed of the boat times .1 hours in that direction.
That would be equal to 20.61552813 * .1 = 2.061552813.
The z component is the result of the x component and the y component.
For speed,the z component is 20.61552813 km/h.
For distance, the z component is 2.061552813 km.
The time it takes to travel the z component is equal to R * T = D which becomes T = D / R which becomes T = 2.061552813 / 20.61552813 = .1 hours.
In .1 hours, the boat has traveled 2 km directly across the river.
In the same .1 hours, the current has pushed the boat .5 km downstream.
In the same .1 hours, the boat has traveled 2.061552813 km taking into account the direction of the boat without the current and the direction of the current.
A picture of these vectors is shown below:
|
|
|