SOLUTION: Use the student aga data and ,apply Chebyshev's theorem and the empirical rule - identify the intervals that will include 68 percent, 95 percent, and 99 percent of the age data. Co

Algebra ->  Probability-and-statistics -> SOLUTION: Use the student aga data and ,apply Chebyshev's theorem and the empirical rule - identify the intervals that will include 68 percent, 95 percent, and 99 percent of the age data. Co      Log On


   

Question 320246: Use the student aga data and ,apply Chebyshev's theorem and the empirical rule - identify the intervals that will include 68 percent, 95 percent, and 99 percent of the age data. Compute and interpret the quartiles and interquartile range for the data.
Student Age
1- 42
2- 35
3- 29
4- 33
5- 33
6- 29
7- 26
8- 48
9- 37
10- 27
11- 47
12- 26

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

On your TI-83 or TI-84
 
Press CLEAR
Press STAT
Press 1
 
Enter the 12 numbers in L1
 
Press STAT
Press the right arrow key to highlight CALC
Press 1
Press ENTER
                 _
Read the mean as x = 34.33333333
Read the standard deviation as Sx=7.784989442
 
Chebyshev's theorem states that
 
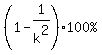%281-1%2Fk%5E2%29%2A%22100%25%22 of the data will lie within k standard
deviations of the mean, where k%3E1.
 
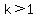Using k=1.1, and the mean and standard deviation above, Chebyshev's 
theorem tells us that AT LEAST 17.3% of the data lies between 25.77 
and 42.897.  In fact 83.3% of it does! 
 
Using k=1.5, and the mean and standard deviation above, Chebyshev's 
theorem tells us that AT LEAST 55.5% of the data lies between 22.66 
and 46.01.  In fact 83.3% of it does!
 
Using k=2, and the mean and standard deviation above, Chebyshev's 
theorem tells us that AT LEAST 75% of the data lies between 18.76 
and 49.90.  In fact 100% of it does!
 
-----------------------------
 
The empirical rule says that if a histogram of the data is 
approximately bell-shaped, like this:
 


then 

1. approximately 68% of the data will fall between 1 standard deviation
below the mean and 1 standard deviation above the mean.

That is, if the given data is approximately bell-shaped, then 68% of
the data should fall between 

34.33333333 - 7.784989442 or 26.54834389
and
34.33333333 - 7.784989442 or 42.11832278

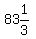Actually 10 of the 12 data values fall between these, so that's 83%261%2F3%

Also
2. approximately 95% of the data will fall between 2 standard deviations
below the mean and 2 standard deviations above the mean.

That is, if the given data is approximately bell-shaped, then about 95% of
the data should fall between 

34.33333333 - 2(7.784989442) or 18.76335445
and
34.33333333 + 2(7.784989442) or 49.90331222

Actually all 12 of data values fall between these, so that's 100%.

Edwin