Question 32022: Amy and Beth live 10 miles from the grocery store. Amy gets in her care and drives to the store at 30mph. At the same time Amy starts Driving, Beth starts walking toward the store at 3mph. Amy spends 1 hour at the store, and then drives home at 30mph. When and where do Amy and Beth meet?
Answer by mbarugel(146)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hello!
I assume here that Amy and Beth live together, or very close to each other.
Clearly, since they start at the same time, and Amy goes faster, they can't meet on the way to the store.
Let's see if they meet at the store.
The store is 10 miles away, and Amy travels at 30 mph. Therefore, she arrives at the store in 10/30 = 1/3 hour (20 minutes). Since she stays one hour, she will stay until 1 hour and 20 minutes have passed since she left her home.
Beth, on the other hand, travels at 3 mph. Therefore, she takes 10/3 hour (3 hours 20 minutes) to get to the store. Therefor, it's impossible for them to meet at the store. It must be that they meet when Amy's returning home.
After 4/3 hour (1 hour and 20 minutes) of leaving her home, Amy begins her journey back home. At this point, Beth has already traveled 4 miles (she's traveled for 4/3 hour at 3 mph).
Now we get the following equations. Starting at 4/3 hours, and calling X to the number of hours that pass AFTER 4/3 hours, Beth's distance from her home is 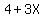 (4 miles that she has already walked plus 3 miles per hour). On the other hand, Amy's distance from her home is (4 miles that she has already walked plus 3 miles per hour). On the other hand, Amy's distance from her home is 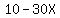 (she starts at 10 miles away, and the distance DECREASES at 30 miles per hour, as she's going back). Therefore, they will meet when: (she starts at 10 miles away, and the distance DECREASES at 30 miles per hour, as she's going back). Therefore, they will meet when:



Therefore, they will meet exactly  hours after leaving home. At this point, Beth will be at hours after leaving home. At this point, Beth will be at  miles away from home. Amy will be at miles away from home. Amy will be at  away from home (so they'll be at the same spot) away from home (so they'll be at the same spot)
I hope this helps!
Get more answers at Online Math Answers.com!
|
|
|