SOLUTION: YOU OWN A COMPUTER STORE SELLING TWO TYPES OF LASER PRINTER. tHE FIRST TYPE A, HAS A COST OF $165 AND YOU MAKE A PROFIT OF $45 ON EACH ONR. THE SECOND TYPE B, HAS A COST OF $110 AN

YOU OWN A COMPUTER STORE SELLING TWO TYPES OF LASER PRINTER. tHE FIRST TYPE A,

HAS A COST OF $165 AND YOU MAKE A PROFIT OF $45 ON EACH ONR. THE SECOND TYPE

B, HAS A COST OF $110 AND YOU MAKE A PROFIT OF $30 ON EACH ONE. YOU EXPECT TO

SELL AT LEAST 100 LASER PRINTERS THIS MONTH AND YOU NEED TO MAKE AT LEAST

$3450 PROFIT ON THEM. A) HOW MANY OF EACH MODEL SHOULD YOU ORDER IF YOU WANT

TO MINIMUM[ize} THE COST? B) WHAT IS THE MINIMUM COST?

--------------------------------------------------------------------

The question reads:

>>...HOW MANY OF EACH MODEL SHOULD YOU ORDER...<< 

So let x = the number of type A printers to order

and y = the number of type B printers to order.

>>...YOU EXPECT TO SELL AT LEAST 100 LASER PRINTERS THIS MONTH...<< 

Translation: x + y > 100

>>...tHE FIRST TYPE A,...YOU MAKE A PROFIT OF $45 ON EACH...<<

>>...THE SECOND TYPE B,...YOU MAKE A PROFIT OF $30 ON EACH ONE.

>>...YOU NEED TO MAKE AT LEAST $3450 PROFIT ON THEM...<<

Translation:  45x + 30y > 3450

>>...tHE FIRST TYPE A, HAS A COST OF $165...<<

>>...THE SECOND TYPE B, HAS A COST OF $110...<<

>>...YOU WANT TO MINIMUM[ize] THE COST...<<

Translation: Minimize C = 165x + 110y

So the problem is:

Minimize C = 165x + 110y, subject to contraints:

    x + y > 100

45x + 30y > 3450

        x > 0

        y > 0

The last two come from the fact that x and y can't be negative. They

limit the graph to the 1st quadrant, i.e., above the x-axis and to the

right of the y-axis.

Now we form the boundary equations by replacing the inequality symbol

in each to an equal sign:

    x + y = 100     [intercepts (0,100) and (100,0]

45x + 30y = 3450    [intercepts (0,115) and (76 2/3, 0)

        x = 0

        y = 0

Draw the graphs

 

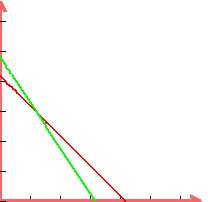
The feasible region is the infinitely large region which is above both

the green and red lines, above the x-axis, and to the right of the y-axis.

Now we find all the corner points of this region.  They are 

(0,115), (30,70), and (100,0) 

The mimimum cost will be the smallest of the values found for C

when C = 165x + 110y is evaluated at each of these corner points:

For (0,115), C = 165x + 110y = 165(0) + 110(115) = $12650 

For (30,70), C = 165x + 110y = 165(30) + 110(70) = $12650

For (100,0), C = 165x + 110y = 165(100) + 110(0) = $16500

The mimimum of these is $12650. That's the answer to (b). Now, since two

adjacent corner points happen to yield this same mimimum cost, then any point

on the line that connects them where both x and y are non-negative integers

will yield that same minimum cost, namely $12650.  So there are 16 possible

answers to (a)



These are



(0,115) which means to order 0 A's and 115 B's 

(2,112) which means to order 2 A's and 112 B's

(4,109) which means to order 4 A's and 109 B's

...

(26,76) which means to order 26 A's and 76 B's

(28,73) which means to order 28 A's and 73 B's

(30,70) which means to order 30 A's and 70 B's



Edwin