|
Question 3198: Derek rakes and bags the leaves of a lawn in 3 hrs. Alferd rakes and bags them in 5 hours. How long will it take to rake and bag the leaves if they do it together?
Answer by drglass(89)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve this problem, you need to identify two things: the form of the answer and the facts you have to solve the problem.
Form of the answer:
The question is asking for the time it would take Derek and Alferd to rake the lawn and bag the leaves, so the answer should look like:
It would take them _____ hours to rake the lawn and bag the leaves.
To make this easier to write, we will treat raking and bagging as one thing, but when we answer the question, we have to remember to include both parts.
Facts:
1) It takes Derek 3 hours to rake the lawn
2) It takes Alferd 5 hours to rake the lawn
Next, we write the facts in a mathematical way:
Let's let the the letter D mean "the speed at which Derek can rake the lawn" so

means Derek can rake  lawns per hour lawns per hour
We can also let A mean "the speed at which Alferd can rake the lawn," so
 lawns per hour. lawns per hour.
Notice that the facts don't relate directly to the problem. They tell us about speed but not time. This makes it a little more difficult to solve because we have to hope we can relate speed to time. Fortunately, we can do exactly that.
With our facts written in a mathematical way, we can solve the problem.
"The speed at which Derek and Alferd can rake the lawn" is written 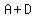 .So our solution begins .So our solution begins
 lawns per hour lawns per hour
We make both fractions take the same denominator by multiplying  by by  and multiplying and multiplying  by by  . This gives us . This gives us
 lawns per hour lawns per hour
This almost answers the question. It tells us that Derek and Alferd can rake  lawns per hour but, we need to know the time it takes them to rake one lawn. Let's call this time t.We can write this mathematically: lawns per hour but, we need to know the time it takes them to rake one lawn. Let's call this time t.We can write this mathematically:
1 lawn raked = (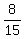 lawns per hour) * ( lawns per hour) * ( hours) hours)
If we divide both sides by  , we get: , we get:
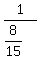 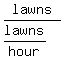 = t hours = t hours
So t = 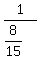 = =  = 1 = 1
So, our answer is:
It would take them 1 hours to rake the lawn and bag the leaves. hours to rake the lawn and bag the leaves.
With practice, you will learn to do these steps by writing the problem mathematically, but for now, keep everything clear by writing it down.
|
|
|
| |