If you have a TI-83 or 84,
From the cleared main screen
Press 2ND
Press VARS
Press 3
you will see this on the screen --> invNorm(
after that type .81,61,10.2) so that you see this on the
screen ---> invNorm(.81,61,10.2)
[If you can't find the comma key it is the key just to the right of x2).
Press ENTER
You will see 69.95454216, which you round to the nearest whole
number 70.
If you are not allowed to use a calculator, then you must go through
the following long process:
Draw a normal curve on the x (not z) axis marking the middle point
as the mean 61. Then mark off units right and left by adding the
standard deviation 10.2 to the mean and the standard deviation to that
to mark points to the right and subtracting 10.2 from the mean to get
points on the left side.
Next we redraw the normal curve with a z-axis of z-scores instead
of an x-axis of "x-scores" (actual values). This graph has z=0
corresponding to x=61, z=1 corresponding to x=71.2, z=2 corresponding
to x=81.4, z=-1 corresponding to 50.8, and z=-2 corresponding to 40.6.
So you see that the z-score is just the number of standard deviations
the corresponding x-score is from the mean.
The area under the entire normal curve is 1. So the area under the
left side of the normal curve is .5. We want to find the value of z
such that 81% or .81 of the area is under the curve to the left of that
z-value. So .5 of the .81 is to the left of z=0 and that leaves
.81 - .5 = .31 for the area on the right of z=0. So we look in the body
of the table and find the nearest value to .31 for the area to the
right of z=0 that we need to make up the rest of the 81%. We find
that .3106 is the closest area value in the table. Then we observe that
.3106 occurs where z = .88. So that is the cut off value we are looking
for. I'll indicate it with a green line at z=.88, just a little to the
left of z=1.
The area under the curve to the left of the green line represents the bottom
81% and the area under the curve to the right of the green line represents
the top 19%.
Now what we have to do is to find the x-score on the x-axis that corresponds
to the z-score of .88 on the z-axis. I'll redraw the normal curve with the
x-axis, keeping the green dividing line:
We can see that the green dividing line is a little to the left of x=71.2.
We calculate that value by using the formula
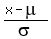which when solved for x is
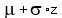So the x-score that corresponds to the z-score .88 is
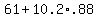
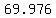[Notice that is slightly different from what the calculator gave.
But that's because we could not find .31 exactly in the table so
the best we could do was to use .3106 instead. The calculator
is more accurate than the table.
However, rounding that to the nearest whole number gives us the
same cut-off score of 70.
Edwin
