Question 319256: This is a former test question. I have made many attempts but cant solve it.
Q.
A car travel at 40 km/hr and can get a range of 400km.
If it travels at 80 km/ hr it is 4 times less fuel efficient.
What is the quickest time the car can travel 240 km hr
A. My answer so far...
the car travels a mixture of high and low speed. The question asks for the "quickest time", but this time will occur when the high speed component of travel is at its maximum (for this range)
So I think to answer the question, i need to find a formula to express the distance traveled (240 km) in terms of distance traveled at low speed and high speed, and then maximize it for high speed travel, yes?
some maths...
lets say fuel tank has T lt
efficiency at low speed = 400/T (km/lt)
efficiency at high speed = 100/T (km/lt) - because 4 times less efficient
then distance traveled = 240 km = distance traveled at slow speed (Ds)+ distance traveled at high speed (Dh)
Ds = (400/T)*Slow liters ( km/lt fuel efficiency * slow travel liters used)
Df = (100/T)*fast liters
After this i get lost in the maths and think maybe i am taking the wrong approach.
Any ideas will help me
Regards
Adam
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! The quickest time the car can travel is going the fastest speed.
.
.
.
You didn't mention it but are you constrained to only use 1 tank of fuel?
Rate*Time=Distance
.
.
.
40 kph Range=400 km
80 kph Range=200 km
.
.
.
First equation, distance traveled at times T1 and T2


.
.
.
Now let's look at efficiency.
We need an equation that relates the fuel usage (liters/hr) to speed (km/hr) and the efficiency (km/liter).
.
.
.
Let's say the tank holds Z liters.
.
.
.
Let's define the fuel rate as Q,
(400 km/Z liter)*Q1(liters/hr)=40 km/hr
 liters/hr liters/hr
.
.
(100 km/Z liters)*Q2(liters/hr)=80 km/hr
 liters/hr liters/hr
.
.



.
.
So now you have a linear programming problem.
You have two constraint equations.
The solution lies on the line,


.
.
.
The feasible region vertices to minimize the function, 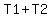 occur at occur at
 , , 
 , , 
and the intersection point of the two lines.

1.
2.
From eq. 1,

Substitute into eq. 2,



.
.
.



Check the function at each point:
 , ,  : :
 , ,  : :
 , , : :
.
.
.
The fastest time occurs when  and and  . .
|
|
|