|
Question 31921: I'm having a hard time understanding the step by step process in factor competely. Here are my answer, but I'm still not comfortable with it, please check my work and point out my errors. Greatly apprecated.Thank you
Factor completely:
x2 – 5x – 14
x^2-5x-7
Factor completely:
4x2 – 36y2
=2x^2-18y^2
=(2x^2- 9y^2)
=(2x^2-3y^2)
Found 2 solutions by benni1013, Earlsdon:
Answer by benni1013(206)   (Show Source): (Show Source):
You can put this solution on YOUR website! Whoa partner I believe you are way off in left field. Let to talk about so lets get started.
Your first question: Factor completely: x^2-5x-14
Fact: A binomial times a binomial equals a trinomial
Ask yourself what factors of negative 14 equals 5?
Answer: 7, -2
So: x^2+7x-2x-14==>x(x+7)-2(x+7)
The same numbers in the parentheses is one of your quantities the one outside is the other==>(x-2)(x+7)
Your second question follows under the special rule of "the difference of two squares" this occurs when the middle term become zero in multiplying two binomials and the format is: (x-y)(x+y)
Back to your problem:(2x-6y)(2x+6y) is your answer.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! The goal in factoring trinomials/binomials, as you have in your problem, is to find the two binomials which, when multiplied together, will result in the given trinomial/binomial. Now not all trinomials/binomials are factorable, but in general, you can nearly always find two such binomials. The trick is to use the right technique for your particular trinomial/binomial.
In the first one  , for example, you have have divided the constant term (14) by 2. Why did you do this? , for example, you have have divided the constant term (14) by 2. Why did you do this?
Here's an approach you might try:
Factor:
 You want to find two binomials of the form You want to find two binomials of the form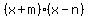 such that: such that:
m X n = -14 and
m + n = -5
Using a bit of trial & error:
2 X (-7) = -14
(-2) X 7 = -14
2 + (-7) = -5 This works!
(-2) + 7 = 5 This doesn't work!
So from the above, m = 2 and n = -7
The factors are:

For you second problem, notice that your binomial is "the difference of two squares". There is a formula for factoring these:

To find the A and B in your binomial, you must take the square root of each term.
 = 2x = 2x
 = 6y = 6y
Now substitute these values for A (2x) and B (6y) into the formula:

I hope this helps!
|
|
|
| |