Question 317630: A farmer has 100 animals consisting of cows, pigs and chickens. He takes the animals to market and sells all of them for $100.
He sells cows for $10
He sells pigs for $3
He sells chickens 2 for $1
How many of each animal does he sell? (no 1/2 animals)
I came up with x+y+z=100 animals...
and 10x+3y+0.5z=100 dollars
I believe this needs another equation but I cannot figure it out. Also we are working with arbitrary numbers in class. Thank You! Scott M.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Cows cost $10, Pigs cost $3, and chickens cost $.50.
He only bought 100 animals and bought at least one of each animal.
He only spent $100. How many of each animal did he buy?
:
Let c = no. of cows; p = no. of pigs; s = no. chickens
:
No. of animals equation:
c + p + s = 100
:
Cows cost $10, Pigs cost $3, and chickens cost $.50.
the $$ equation:
10c + 3p + .5s = 100
:
We have two equations but 3 unknowns, however, we know there can't very many cows,
After trying a couple values for no. of cows, came up with 5 cows,
they're worth $50, our two equations then are:
:
p + s = 100 - 5
p + s = 95
and
3p + .5s = 100 - 50
3p + .5s = 50
:
Multiply the 1st equation by 3 and subtract the 2nd equation:
3p + 3s = 285
3p + .5s = 50
---------------- subtracting eliminates p
0p + 2.5s = 235
s = 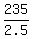
s = 94 chickens
:
Find pigs
p + 94 = 95
p = 95 - 94
p = 1 pig
:
We have then: 5 cows, 1 pig, 94 chicken
;
;
Check in the cost equation
10(5) + 3(1) + 94(.5) =
50 + 3 + 47 = $100
|
|
|