Question 317209: What is the area of the region enclosed by the graphs of y = 2│x − 3│ − 2
and y = 4 − 2│x − 2│?
Found 2 solutions by Fombitz, Edwin McCravy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! What is the area of the region enclosed by the graphs of y = 2│x − 3│ − 2
and y = 4 − 2│x − 2│?
The other tutor's solution is correct but I think you should
calculate the vertices rather that assume they are exactly as
they look.
Let's graph it:
 The region looks like a parallelogram.
We need to find the corner points, which
are the two vertices and the two points of intersection
To find the vertex of
The region looks like a parallelogram.
We need to find the corner points, which
are the two vertices and the two points of intersection
To find the vertex of  we set the part
in the absolute value = 0 we set the part
in the absolute value = 0
 and solve for x
and solve for x
 And we substitute this in
And we substitute this in





 So the vertex of
So the vertex of  is (3,-2).
To find the vertex of y=4-2abs(x-2)}}} we also set the part
in the absolute value = 0 is (3,-2).
To find the vertex of y=4-2abs(x-2)}}} we also set the part
in the absolute value = 0
 and solve for x
and solve for x
 And we substitute this in
And we substitute this in





 So the vertex of
So the vertex of  is (2,4).
Now we find the other two vertices of the figure
We solve the system is (2,4).
Now we find the other two vertices of the figure
We solve the system
 Since the right sides both equal to y, set them equal:
Since the right sides both equal to y, set them equal:
 We can divide every term through by 2 without getting fractions,
so we do so:
We can divide every term through by 2 without getting fractions,
so we do so:
 Add 1 to both sides:
Add 1 to both sides:
 There are four cases to consider:
1.
There are four cases to consider:
1. 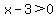 and and  which is the same as
which is the same as
 and and  which is the same as
which is the same as

 becomes
becomes




 Substitute in
y=2abs(x-3)-2
y=2abs(4-3)-2
y=2abs(1)-2
y=2(1)-2
y=0
So one point of intersection is (4,0)
2.
Substitute in
y=2abs(x-3)-2
y=2abs(4-3)-2
y=2abs(1)-2
y=2(1)-2
y=0
So one point of intersection is (4,0)
2. 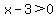 and and 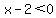 which is the same as
which is the same as
 and and  That's a contradiction, so we ignore this case.
3.
That's a contradiction, so we ignore this case.
3.  and and  which is the same as
which is the same as
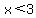 and and  which is the same as
which is the same as
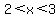
 becomes
becomes



 Thats a contradiction too. So we ignore this case
4.
Thats a contradiction too. So we ignore this case
4.  and and 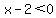 which is the same as
which is the same as
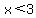 and and  which is the same as
which is the same as

 becomes
becomes






 Substitute in
y=2abs(x-3)-2
y=2abs(1-3)-2
y=2abs(-2)-2
y=2(2)-2
y=4-2
y=2
So the other point of intersection is (1,2)
So the area we want to find is the area of the polygon whose vertices
are (1,2), (3,-2), (4,0), and (2,4) figure:
Substitute in
y=2abs(x-3)-2
y=2abs(1-3)-2
y=2abs(-2)-2
y=2(2)-2
y=4-2
y=2
So the other point of intersection is (1,2)
So the area we want to find is the area of the polygon whose vertices
are (1,2), (3,-2), (4,0), and (2,4) figure:
 Since the polygon is convex (doesn't "sink in"
anywhere). we use the determinant formula, whose
rows are the coordinates in counter-clockwise order, with the first
row repeated at the bottom:
Since the polygon is convex (doesn't "sink in"
anywhere). we use the determinant formula, whose
rows are the coordinates in counter-clockwise order, with the first
row repeated at the bottom:
    To expand it add the sum of the products of the diagonals going down
to the right and subtract the sum of the products of the diagonals
going up to the right:
To expand it add the sum of the products of the diagonals going down
to the right and subtract the sum of the products of the diagonals
going up to the right:
      [ [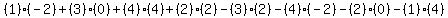 ] ]  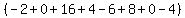   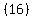   Edwin
Edwin
|
|
|