Question 316258: You wish to replenish your stock of dishes by purchasing 250 sets for your restaurant. You have two dish designs from which to choose from. One design cost $20 per set and the other $45 per set. You only have $6,800 to spend, how many of each design should you order. x=the number of $20 dishes and y=the number of $45 dishes. Could you help me solve each equation and explain how to check solutions for both equations?
Answer by moshiz08(60)   (Show Source):
You can put this solution on YOUR website! I think you might have double posted this question, it's OK, I hope this is helpful.
x=the number of $20 dishes
y=the number of $45 dishes
Since you want to purchase 250 total,  . We can rewrite this as  . (eq1)
Now suppose you buy 4 of the $20 dishes and 2 of the $45 dishes. The you spend 4*$20 = $80 on the four $20 dishes and 2*$45= $90 on the two $45 dollar dishes.
In general, you multiply. So if you buy x dishes for $20, you spend 20*x dollars on them. Then if you buy y dishes for $45, you spend 45*y on them. The total amount of money you spend is 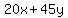 , and since we know that you have $6800, we get  . (eq2)
Let us substitute our equation for y given by (eq1) into (eq2).
Distributing the 45 gives
Combining like terms gives
Add 25x to both sides to get
Subtract 6800 from both sides to get
Divide both sides by 25 to get
Thus, from (eq1) we can get  . So you should buy 178 of the $20 dish sets and you should buy 72 of the $45 dish sets.
Now let us check. The total number of dish sets you buy is 178 + 72 which is a total of 250 as you requested. The amount of money you pay is a total of 178 * $20 = $ 3560 for the $20 dishes and 72 * $45 = $3240 for the $45 dishes. This means you spend #3560 + $3240 = $6800.
Good luck on the restaurant business!
Take care,
Mo
|
|
|
