SOLUTION: write in a+bi form 1). {{{(4+5i)/(6+i)}}} 2). {{{14/i}}}

Form the conjugate of 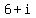 by changing the sign of the term
containing  and leaving the sign of the first term.

Thus the conjugate of 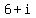 is .

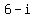Place that conjugate over itself, like this ,
which just equals 1, and so we can now multiply the original
expression by that without changing its value:





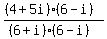Using FOIL on top and bottom:



Combining like terms (the middle terms cancel in the bottom)



Replace  by 



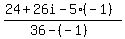Simplify:





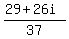Make two fractions, and write the  as multiplied on the right of
the second fraction, so it will be in the standard form :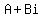



---------------

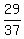
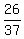
2). 

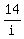You only need to multiply that by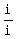 





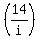
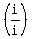
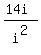Replace the  by 





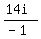
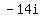Edwin