SOLUTION: {{{ (32^-1^4)^-4^5 }}} the exponents are supposed to be negative fractions ^-1/4 and ^-4/5 please help :)

Algebra ->  Exponents-negative-and-fractional -> SOLUTION: {{{ (32^-1^4)^-4^5 }}} the exponents are supposed to be negative fractions ^-1/4 and ^-4/5 please help :)      Log On


   

Question 314459: 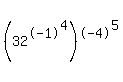+%2832%5E-1%5E4%29%5E-4%5E5+
the exponents are supposed to be negative fractions ^-1/4 and ^-4/5
please help :)
Found 2 solutions by texttutoring, Theo:
Answer by texttutoring(324) About Me  (Show Source):
You can put this solution on YOUR website!
Multiply the exponents:

-1/4 * -4/5 = 1/5

You are left with
32^(1/5)

or in other words, what is the 5th root of 32?

The answer is 2.

Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
If I understand you correctly, your expression should look like this:

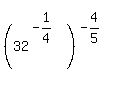
%2832%5E%28-1%2F4%29%29%5E%28-4%2F5%29

Because these is a cropping problem with the formula generator when fractional exponents are used, I will make decimal equivalents to allow you to see what's happening better.

1%2F4 is equivalent to .25

4%2F5 is equivalent to .8

Your expression becomes:

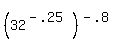
%2832%5E%28-.25%29%29%5E%28-.8%29

To solve this problem, you will use two of the rules of exponentiation.

The first rule is x%5E%28-n%29+=+1%2Fx%5En

The second rule is %28x%5Em%2Fy%5En%29%5Ek+=+x%5E%28m%2Ak%29%2Fy%5E%28n%2Ak%29

When you have nested parentheses, you always resolve the inner parentheses before resolving the outer parentheses.

We will follow that rule.

Your expression to be simplified is 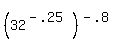%2832%5E%28-.25%29%29%5E%28-.8%29

Using the first rule to resolve the inner parentheses, we get:


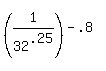
%281%2F32%5E.25%29%5E%28-.8%29

Using the first rule again to resolve the remaining expression, we get:


%281%2F%281%2F32%5E.25%29%5E%28.8%29%29

Using the second rule, our expression becomes:


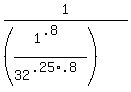
1%2F%28%281%5E%28.8%29%2F32%5E%28.25%2A.8%29%29%29

This simplifies further to:

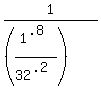
1%2F%28%281%5E%28.8%29%2F32%5E%28.2%29%29%29

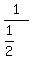Since 1%5E.8+=+1 and 32%5E%28.2%29+=+2, then our expression becomes 1%2F%281%2F2%29 which is equal to 2.

Our expression resolves to 2.

You can confirm this answer is correct by plugging the original expression into your calculator and then plugging the final expression into your calculator to see that you get the same answer.

Use the decimal equivalents of the fractional exponents since they are easier to work with, although you should know how to handle the fractions as well.

Your original expression with the decimal equivalents of the fractional exponents is:

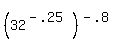%2832%5E%28-.25%29%29%5E%28-.8%29 which resolves to 2.

Your final expression with the decimal equivalents of the fractional exponents is:

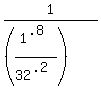1%2F%28%281%5E%28.8%29%2F32%5E%28.2%29%29%29 which resolves to 2.

Both expressions resolve to 2 which indicates that the simplification process worked as expected.

If I were to do this by hand, the progression would look like this:

picture not found