SOLUTION: An equilateral triangle has an area of 300square root of 3. Find the apothem. My teacher said that there is a formula that can be used to find this. I have looked and looked

Algebra ->  Triangles -> SOLUTION: An equilateral triangle has an area of 300square root of 3. Find the apothem. My teacher said that there is a formula that can be used to find this. I have looked and looked      Log On


   

Question 31363: An equilateral triangle has an area of 300square root of 3. Find the apothem.

My teacher said that there is a formula that can be used to find this. I have looked and looked but have not been successful yet. She said it has to do with the connection between the area and perimeter of equilateral triangles. I tried to find the perimeter of the triangle by using the area formula A=1/2bh. I was unable to get anywhere close to the area. I don't know what else to try. Could you please help me?
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Well, first, let's see the definition of an apothem of a regular polygon, of which, an equilateral triangle is certainly an example:
"An apothem of a regular polygon is a line drawn from its centre perpendicular to one of its sides" This is also the radius of the inscribed circle.
The formula for finding an apothem of a regular polygon is:
r+=+%281%2F2%29%28s%29cot%28180%2Fn%29
Where:
r = is the length of the apothem.
s = the length of one side of the regular polygon (equilateral triangle).
n = the number of sides in the regular polygon (3).
One minor problem is...you don't know the length of one side (s) of the equilateral tringle!
Not to worry however because you do know the area and you can use Heron's formula for finding the length of the side of the equilateral triangle.
Heron's formula, which gives the area of a triangle as a function of the length of the sides is:
A+=+sqrt%28s%28s-a%29%28s-b%29%28s-c%29%29
Where:
s = the semi-perimeter of the triangle.
a, b, c, are the lengths of the sides of the triangle.
But, in an equilateral triangle, a = b = c and 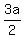s+=+%28a%2Bb%2Bc%29%2F2 = 3a%2F2
So, let's find the length (a) of one side of the triangle using Heron's formula A+=+sqrt%28s%28s-a%29%28s-b%29%28s-c%29%29and the known area of the triangle300sqrt%283%29
Rewrite Heron's formula for the case of an equilateral triangle where s+=+3a%2F2
A+=+sqrt%28%283a%2F2%29%28%283a%2F2%29-a%29%5E3%29 Simplify.
A+=+sqrt%28%283a%2F2%29%28a%2F2%29%5E3%29
A+=+sqrt%28%283a%2F2%29%28a%5E3%2F8%29%29
A+=+sqrt%283a%5E4%2F16%29
A+=+%28a%5E2%2F4%29sqrt%283%29 But the area of the triangle is given as A+=+300sqrt%283%29, so:
300sqrt%283%29+=+%28a%5E2%2F4%29sqrt%283%29 Simplifying, we get:
300+=+a%5E2%2F4 Solving for a, the length of the side of the triangle:
a%5E2+=+4%28300%29
a%5E2+=+1200 Taking the square root of both sides.
a+=+20sqrt%283%29
Now we can substitute this for s in the formula for the apothem.
r+=+%281%2F2%2920sqrt%283%29cot%28180%2F3%29 Simplifying.
r+=+10sqrt%283%29cot%2860%29
r+=+10sqrt%283%29%280.577%29
r+=+5.77sqrt%283%29 This is the length of the apothem.