|
Question 313391: How many three digit numbers are such that the product of their digits is 120?
Found 3 solutions by Fombitz, toidayma, MathTherapy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Look at first digits.
100 series numbers are out since 199 gives the largest product=81<120.
200 series numbers are also out since no two digits multiplied together produce 60.
300 series numbers remaining digits need a product of 40: 358,385
400 series numbers remaining digits need a product of 30: 456,465
500 series numbers remaining digits need a product of 24: 524,538,542,583
600 series numbers remaining digits need a product of 20: 545,554
700,800,900 series numbers are out since 7,8,and 9 do not evenly divide 120.
Counting them up gives 10 3 digit numbers.
.
.
.
EDIT
Oops!
800 series numbers remaining digits need a product of 15: 835, 853
That adds 2.
SO there are  3 digit numbers that whose product is 120. 3 digit numbers that whose product is 120.
Answer by toidayma(44)   (Show Source): (Show Source):
You can put this solution on YOUR website! Firstly, we have 120 = 2^3*3*5
since each digit is smaller than 10, therefore, one digit must be 5. We have 2 digits left with product of 2^3*3
there are only two case for one digit that has the factor of 3: 3, 3*2 (3*2^2 is larger than 9)
So there are totally two 3-digit sets that has the product of 120: (5,3,8) and (5,6,4)
With each set, we have 3! different digits that satisfied the product of the three digits is 120.
Thus, there are totally 2*3! = 12 such digits.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many three digit numbers are such that the product of their digits is 120?
Since the product of these numbers end with a 0 (zero), and the digits must be from 1 Ė 9 (canít be 0, because the product would be 0), then one of the 3 digits must be a 5, since the only digit that yields a product with a units digits of 0 is 5.
Dividing 120 by 5, we get 24.
Now, the factors of 24, between 1 & 9, are 8 & 3, and 6 & 4. This means that the digits that multiply to 120 are 583 and 564. Since there are 6 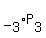 , or , or 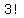 ways that we can arrange the digits in 583 and 6 ways that we can arrange the digits in 583 and 6 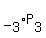 , or , or 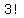 ways that we can arrange the digits in 564, there are 12 (6 + 6) ways that we can arrange both sets of digits. This means that there are ways that we can arrange the digits in 564, there are 12 (6 + 6) ways that we can arrange both sets of digits. This means that there are  3-digit numbers that can be formed whose product is 120. 3-digit numbers that can be formed whose product is 120.
|
|
|
| |