Question 312755: A bag contains 5 yellow marbles, 16 green marbles, and 2 red marbles. What is the chance of drawing a red marble? If a red marble is drawn the first time and then a second marble is drawn without replacement, what is the probability of drawing a yellow marble? Give solutions exactly in reduced fraction from separated by a comma?
I do not have a clue?
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! 5 yellow, Y
16 green, G
2 red, R
Add them up to get 23 total marbles.
P(event)=number of outcomes of that event/total outcomes.
.
.
.
1. So the chance of drawing a red marble is,
P(R)=Red Marbles/Total Marbles=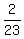
.
.
.
Once you chose a red marble and don't replace it, the marble count changes, you then have 1 red marble and 22 total marbles. The probability of picking a red then changes to
P(R)=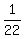 . .
The total probability of picking two reds in a row is the product of both probabilities.
P(2 R)=
.
.
.
P(Y)=Yellow marbles/Total marbles=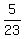
.
.
.
Just for fun,
P(G)=Green marbles/Total marbles=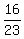 . .
Also note,
P(Y)+P(R)+P(G)=
which means that picking a marble gives you 100% chance of picking either a yellow one, a red one, or a green one, since those are the only choices available.
|
|
|