SOLUTION: Is it possible for x=3 to be in the domains of the functions: 1. {{{q(x)=(2x^2)/(x-3)}}} 2. {{{T(x)= y^2-x}}}, Explain why or why not for each of the above funct

Algebra ->  Functions -> SOLUTION: Is it possible for x=3 to be in the domains of the functions: 1. {{{q(x)=(2x^2)/(x-3)}}} 2. {{{T(x)= y^2-x}}}, Explain why or why not for each of the above funct      Log On


   

Question 312743: Is it possible for x=3 to be in the domains of the functions:

1. q%28x%29=%282x%5E2%29%2F%28x-3%29
2. T%28x%29=+y%5E2-x,
Explain why or why not for each of the above functions? What are the domains of q(x) and T (x)
HELP I AM CONFUSED!!!!!
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

The domain of a function is the set of all numbers that can be substituted
for x that will produce a number for f(x) or y.

You cannot substitute any number for x if it will cause a denominator to be 0.

Is it possible for x=3 to be in the domains of the functions:

1. q%28x%29=%282x%5E2%29%2F%28x-3%29

If you substitute 3 for x in that, you get

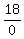   q%283%29=%282%2A3%5E2%29%2F%283-3%29=%282%2A9%29%2F0=18%2F0

Eighteen cannot be divided by zero!  18%2F0 has no meaning whatsoever.
It is not any number.  Therefore we are forbidden to substitute 3 for x.
So 3 cannot be part of the domain.  However every other number is in the
domain.

2. T%28x%29=+y%5E2-x

If we substitute 3 for x in that

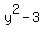   T%283%29=y%5E2-3

y%5E2-3 will never have a zero in the denominator, so for any
value we choose for x or for y, that will produce a number for T.  3 is in
the domain of T as well as every other number.

Edwin