Question 312473: simplify the following radical expression:
3 sqrt () -216x^2/x^2
a) sqrt() -6x
b)-6
c)-6 sqrt()x
d) 6 sqrt()-x
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! This one is really hard for me to understand what your problem was. I'm inclined to think perhaps instead of 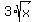 , which is actually read "3 times the square root of x," you probably mean  which is read the "cube root of x."
Next, it's not clear what is in the radical sign. Again, I'm going to guess what I think it is, based upon your multple choice answers.
If this is the problem: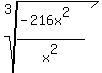 
The fraction reduces first to  .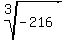
Now, since 6^3= 216, and (-6)^3 = -216, the cube root of -216 is -6. The answer is b. However, if I did not interpret your problem the way it should be stated, you will have to repost the problem.
If you or anyone needs extra help with the Radicals, please see my own website. Click on my tutor name "Rapalje" anywhere in algebra.com. On my information page, click on the link to my Homepage. Once you find my Homepage, look for the link "Basic, Intermediate, and College Algebra: One Step at a Time." Then choose "Basic Algebra", and look in Chapter 5, or choose "Intermediate Algebra" and look in "Chapter 3." There you will find a detailed explanation of radicals, complete with examples, exercises, and most importantly, ALL of the answers. Many of the exercises in these sections are explained IN COLOR in the corresponding "Math in Living Color" pages. My own students used to think my explanations were a LOT easier to understand than the traditional textbooks. You might like my website for an alternative explanation, or for extra problems for practice!
I also have a FREE video of me teaching my class on this topic a few years ago. From my Homepage, look for the link that says "Rapalje Videos in Living Color". There is a video in BOTH "Basic Algebra" and "Intermediate Algebra" for Radicals. It's all FREE.
If you get tired of math, then see the Joke Page!! If you like it please recommend it to friends.
Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Altamonte Springs Campus
|
|
|
