SOLUTION: Solve. What is the solution set? (x+6)(x-4)(x+4)>0

Algebra ->  Inequalities -> SOLUTION: Solve. What is the solution set? (x+6)(x-4)(x+4)>0      Log On


   

Question 312422: Solve. What is the solution set?
(x+6)(x-4)(x+4)>0
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Break up the number line into 4 regions,
Region 1: (-infinity,-6)
Region 2: (-6,-4)
Region 3: (-4,4)
Region 4: (4,infinity)
Pick a point in each region (not the endpoints) and test the inequality.
If the inequality is true, that region is part of the solution set.
.
.
Region 1, let x=-10
+%28x%2B6%29%28x-4%29%28x%2B4%29%3E0
+%28-10%2B6%29%28-10-4%29%28-10%2B4%29%3E0
%28-4%29%28-14%29%28-6%29%3E0
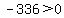
-336%3E0
False
.
.
Region 2, let x=-5
+%28x%2B6%29%28x-4%29%28x%2B4%29%3E0
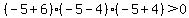
+%28-5%2B6%29%28-5-4%29%28-5%2B4%29%3E0
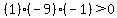
%281%29%28-9%29%28-1%29%3E0
9%3E0
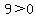
True
.
.
Region 3, let x=0
+%28x%2B6%29%28x-4%29%28x%2B4%29%3E0
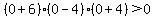
+%280%2B6%29%280-4%29%280%2B4%29%3E0
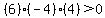
%286%29%28-4%29%284%29%3E0
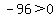
-96%3E0
False
.
.
Region 4, let x=5
+%28x%2B6%29%28x-4%29%28x%2B4%29%3E0
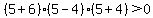
+%285%2B6%29%285-4%29%285%2B4%29%3E0
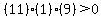
%2811%29%281%29%289%29%3E0
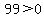
99%3E0
True
So then the solution includes Regions 2 and 4.
(-6,-4)U(4,infinity)