Please help! I am lost in how to figure this out:

That's the same as
 Plot some points:
(-2,-4), (-1,4), (0,8), (1,8), (2,4), (3,-4)
and get this graph:
Plot some points:
(-2,-4), (-1,4), (0,8), (1,8), (2,4), (3,-4)
and get this graph:

This one has several parts..
The x coordinate of the vertex?
Learn the formula:
The x-coordinate of  is
is 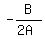 Compare
Compare
 to
to
 and observe that
and observe that  ,
,  ,
,  Then substitute and get
Then substitute and get

The y coordinate of the vertex?
Learn the rule: To get the y-coordinate of the vertex,
after finding the x-coordinate of the vertex, substitute
the value of the x-coordinate of the vertex x in the original
equation:




 So the y coordinate of the vertex is
So the y coordinate of the vertex is  or
or 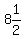 That makes the vertes (
That makes the vertes ( ,
,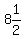 ), or (0.5,8.5)
and we see that looks right according to the graph:
), or (0.5,8.5)
and we see that looks right according to the graph:

The equation of the line of symmetry?
Learn the rule that the equation of the line of symmetry
is always the vertical line whose equation is
x = the x-coordinate of the vertex
So the axis of symmetry has the equation
 or
or  which is a vertical line
which is a vertical line  a unit right of the y-axis
and parallel to it (vertical), and when we graph it (in green,
a unit right of the y-axis
and parallel to it (vertical), and when we graph it (in green,
 and we see that this vertical line whose equation is
and we see that this vertical line whose equation is  ,
bisects the parabola.
,
bisects the parabola.
The maximum/minimum of f(x)?
Learn that the maximum or minimum value is the y-coordinate of
the vertex.
The maximum or minimum point is the same as the vertex.
To determine whether or not it is a maximum or a minimum
we need to know whether the parabola opens upward or downward.
To determine this we look at the coefficient of  .
If it is positive then the parabola opens upward and the
vertex is a minimum point. If it is negative, the parabola
opens downward and the vertex is a maximum.
.
If it is positive then the parabola opens upward and the
vertex is a minimum point. If it is negative, the parabola
opens downward and the vertex is a maximum.
 Here we see that the coefficient of
Here we see that the coefficient of  is negative and
that the parabola opens downward, so the vertex is a maximum.
We knew it opened downward because we graphed it, but we
would have known it opened downward even if we had not
graphed it because the coefficient of
is negative and
that the parabola opens downward, so the vertex is a maximum.
We knew it opened downward because we graphed it, but we
would have known it opened downward even if we had not
graphed it because the coefficient of  is negative.
is negative.
Is the value of  maximum or minimum?
maximum or minimum?
It is a maximum as we have just seen.
Thanks!