SOLUTION: vector A=3i+4j is a vector in xy plane, vector B is a vector perpendicular to vector A, what will be the vector C equal to,which has projections 1 and 2 along vectors A and B?

Algebra ->  Expressions-with-variables -> SOLUTION: vector A=3i+4j is a vector in xy plane, vector B is a vector perpendicular to vector A, what will be the vector C equal to,which has projections 1 and 2 along vectors A and B?      Log On


   

Question 31236: vector A=3i+4j is a vector in xy plane,
vector B is a vector perpendicular to vector A,
what will be the vector C equal to,which has projections 1 and 2 along vectors A and B?
Found 2 solutions by longjonsilver, venugopalramana:
Answer by longjonsilver(2297) About Me  (Show Source):
You can put this solution on YOUR website!
if vector B is perpendicular to vector A and A is solely in the x-y plane then vector B has to be solely in the z-plane, so its vector is B=ck...some value of k... we do not know where in the z-plane it lies.

So, C = 3i+4j+ck

I think this is what you require.

jon.
------------------------------------------------------------------
OK, after your reply, B is also in the xy plane: my mistake, sorry.

OK, in the xy plane, a.b = 0 for 2 orthogonal vectors.
we have 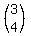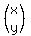%28matrix%282%2C1%2C+3%2C4%29%29.+%28matrix%282%2C1%2C+x%2Cy%29%29+ = 0

so, 3x+4y=0

Now, if both terms were 12 and one negative, then we would have zero. So, how about x=4 and y=-3... that would equal zero.

So, 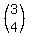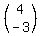+%28matrix%282%2C1%2C+3%2C4%29%29+.+%28matrix%282%2C1%2C4%2C-3%29%29+ = 0 holds true

So, C = 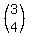+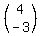%28matrix%282%2C1%2C+3%2C4%29%29+++%28matrix%282%2C1%2C4%2C-3%29%29+
+%28matrix%282%2C1%2C%283%2B4%29%2C%284-3%29%29%29+
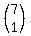
+%28matrix%282%2C1%2C7%2C1%29+%29

this is one version of the answer, since the scalar product could also have been: 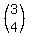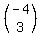+%28matrix%282%2C1%2C+3%2C4%29%29+.+%28matrix%282%2C1%2C-4%2C3%29%29+ = 0

in which case, B would be 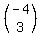+%28matrix%282%2C1%2C-4%2C3%29%29+. And hence C would be:
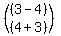
+%28matrix%282%2C1%2C%283-4%29%2C%284%2B3%29%29%29+
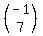
+%28matrix%282%2C1%2C-1%2C7%29%29+

either is correct.
Jon

Answer by venugopalramana(3286) About Me  (Show Source):
You can put this solution on YOUR website!
vector A=3i+4j is a vector in xy plane,
vector B is a vector perpendicular to vector A,
what will be the vector C equal to,which has projections 1 and 2 along vectors A and B?
LET C BE Pi+Qj....
PROJECTION OF C ALONG A =1=A.C/|A|=(3i+4j).(Pi+Qj)/|(3i+4j)
=(3P+4Q)/SQRT.(3^2+4^2)=(3P+4Q)/5=1
3P+4Q=5....................................I
BUT PROJECTION OF C ALONG A =1=|C|*COS(X) WHERE X IS THE ANGLE BETWEEN VECTORS A AND C.
HENCE COS(X)=1/|C|
SINCE B IS PERPENDICULAR TO A WE HAVE ANGLE BETWEEN C AND B =90-X
PROJECTION OF C ALONG B =2=|C|*COS(90-X)=|C|*SIN(X)
SQUARING WE GET …..4=|C|^2*{SIN(X)}^2 = |C|^2*{1-(COS(X))^2}=|C|^2*{1-1/|C|^2}=|C|^2-1……………
|C|^2=4+1=5
P^2+Q^2=5…………………………..II
SUBSTITUTING FOR Q FROM EQN.1,WE GET
P^2+(5-3P)^2/4^2=5
16P^2+25+9P^2-30P=80
25P^2-30P-55=0
5P^2-6P-11=0
5P^2-11P+5P-11=0
P(5P-11)+1(5P-11)=0
(P+1)(5P-11)=0
P=-1…..OR…….11/5
FROM EQN.I,WE GET
Q=(5-3P)/4=(5+3)/4=2……..OR………(5-3*11/5)/4=-2
HENCE VECTOR C IS ……
-i+2j…..OR…….11i/5-2j
WE FIND BY CROSS CHECKING THAT 11i/5-2j IS AN EXTRANEOUS SOLUTION NOT COMPATILE WITH |C|=SQRT.5.
HENCE VECTOR C IS ……-i+2j