We don't have time to do all those for you. We will do just the
first one. But here are the steps to follow on all of them.
a) identify it as odd or even
Substitute -x for +x and simplify. If the expression on the
right can be simplified so that it is exactly the same as the
original expression, then the function is said to be even. If
it can be simplified so that it is exactly the same as the
original expression multiplied by -1, then it is said to
be an odd function. If it cannot be simplied to either be the
same as the original or the original multiplied by -1, then it is
neither even nor odd.
A function is even when it is symmetrical about the y axis, and
is odd when it is symmetrical about the origin.
Use the identities:
 and
and  b) give the period
y = Asin(Bx + C) + D and y = Acos(Bx + C) + D
has period
b) give the period
y = Asin(Bx + C) + D and y = Acos(Bx + C) + D
has period 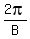 c) give the amplitude, the minimum and maxium
y = A sin(Bx + C) + D or y = Acos(Bx + C) + D
has amplitude |A|, the minimum value is D - |A||,
the maximum value is D + |A|
d) graph the function.
We plot points at x = 0, x =
c) give the amplitude, the minimum and maxium
y = A sin(Bx + C) + D or y = Acos(Bx + C) + D
has amplitude |A|, the minimum value is D - |A||,
the maximum value is D + |A|
d) graph the function.
We plot points at x = 0, x = 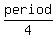 ,
,  ,
, 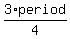 , and
, and  and connect them with an oscillating curve.
You can then extend it indefinitely left and right.
Here is the first one only If you can't do the second one
using the method given above, then post again asking how.
1. y = sin(2x)
a) identify it as odd or even
Substitute -x for +x and simplify.
y = sin[2(-x)]
y = sin[-2x]
Using the identity
y = -sin(2x)
This function is odd because it simplifies to
the original y = sin(2x) multiplied by -1
A function is even when it is symmetrical about the y axis, and
is odd when it is symmetrical about the origin.
b) give the period
y = sin(2x) is the same as
y = 1sin(2x + 0) + 0, which compares to
y = Asin(Bx + C) + D
with A=1, B=2, C=0, D=0
It has period
and connect them with an oscillating curve.
You can then extend it indefinitely left and right.
Here is the first one only If you can't do the second one
using the method given above, then post again asking how.
1. y = sin(2x)
a) identify it as odd or even
Substitute -x for +x and simplify.
y = sin[2(-x)]
y = sin[-2x]
Using the identity
y = -sin(2x)
This function is odd because it simplifies to
the original y = sin(2x) multiplied by -1
A function is even when it is symmetrical about the y axis, and
is odd when it is symmetrical about the origin.
b) give the period
y = sin(2x) is the same as
y = 1sin(2x + 0) + 0, which compares to
y = Asin(Bx + C) + D
with A=1, B=2, C=0, D=0
It has period  c) give the amplitude, the minimum and maxium
The amplitude is |A| = |2| = 2, the minimum value is D - |A| = 0 - 2 = -2,
the maximum value is D + |A| = 0 + 2 = 2,
d) graph the function.
We plot points at x = 0, x =
c) give the amplitude, the minimum and maxium
The amplitude is |A| = |2| = 2, the minimum value is D - |A| = 0 - 2 = -2,
the maximum value is D + |A| = 0 + 2 = 2,
d) graph the function.
We plot points at x = 0, x =  ,
,  ,
,  , and
, and 
 So the five points to plot are (0,0), (
So the five points to plot are (0,0), ( ,1), (
,1), ( ,0), (
,0), (  ,0), and (
,0), and ( ,0)
and connect them with an oscillating curve:
,0)
and connect them with an oscillating curve:
 and if you like you can extend the graph left and right indefinitely,
like this:
and if you like you can extend the graph left and right indefinitely,
like this:
 Try the others on your own, following the rules given above.
and if you have trouble, post again.
Edwin
Try the others on your own, following the rules given above.
and if you have trouble, post again.
Edwin