SOLUTION: How do I write the solution set of {x| } for (x+20)(x -10)(x+11)>0.

Algebra ->  Inequalities -> SOLUTION: How do I write the solution set of {x| } for (x+20)(x -10)(x+11)>0.       Log On


   

Question 309805: How do I write the solution set of {x| } for (x+20)(x -10)(x+11)>0.
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
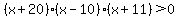
How do I write the solution set of {x| } for %28x%2B20%29%28x-10%29%28x%2B11%29%3E0

Find all the critical values by setting each of the factors on the
left = 0

x + 20 = 0 gives critical value x = -20

x - 10 = 0 gives critical value x = 10

x + 11 = 0 gives critical value x = -11

Mark them on a number line:

----------o-----------------------------------o-----------------------------------------------------------------------------------o---------
-22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7   8   9  10 11 12 13

Choose a value left of -20, the left-most critical value,
say x = -21.  Test it by substituting in the inequality:

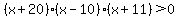
%28x%2B20%29%28x-10%29%28x%2B11%29%3E0
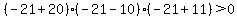
%28-21%2B20%29%28-21-10%29%28-21%2B11%29%3E0
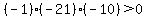
%28-1%29%28-21%29%28-10%29%3E0
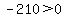-210%3E0

That is false so we DO NOT shade the part of the number line
left of -20.  So we still have the unshaded number line

----------o-----------------------------------o-----------------------------------------------------------------------------------o---------
-22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7   8   9  10 11 12 13

Choose a value between -20 and -11, say x = -12.  Test it by substituting in the inequality:

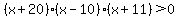
%28x%2B20%29%28x-10%29%28x%2B11%29%3E0
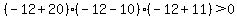
%28-12%2B20%29%28-12-10%29%28-12%2B11%29%3E0
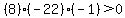
%288%29%28-22%29%28-1%29%3E0
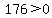176%3E0

That is true so we DO shade the part of the number line between -20 and
-11.  So we have:

----------o===================================o-----------------------------------------------------------------------------------o--------->
-22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7   8   9  10 11 12 13

Choose a value between -11 and 10, say x = 0.  Test it by substituting in the inequality:

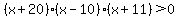
%28x%2B20%29%28x-10%29%28x%2B11%29%3E0
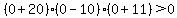
%280%2B20%29%280-10%29%280%2B11%29%3E0
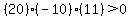
%2820%29%28-10%29%2811%29%3E0
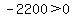-2200%3E0

That is false so we DO NOT shade the part of the number line between -20 and
-11.  So we still have:

----------o===================================o-----------------------------------------------------------------------------------o--------->
-22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7   8   9  10 11 12 13

Choose a value right of 10, the right-most critical value,
say x = 11.  Test it by substituting in the inequality:

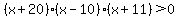
%28x%2B20%29%28x-10%29%28x%2B11%29%3E0
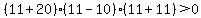
%2811%2B20%29%2811-10%29%2811%2B11%29%3E0
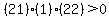
%2821%29%281%29%2822%29%3E0
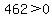462%3E0

That is true so we DO shade the part of the number line to the right of
10.  So we have:

----------o===================================o-----------------------------------------------------------------------------------o=========>
-22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10  -9  -8  -7  -6  -5  -4  -3  -2  -1   0   1   2   3   4   5   6   7   8   9  10 11 12 13


In set-builder notation the solution set is written:

{x | -20 < x < -11 OR x > 10}

In interval notation the solution set is written:

(-20,-11) U (10,infinity)

Edwin