SOLUTION: what is one possible value of x for which x < 2 < 1/x ?

 is a possible value for x because



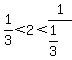Inverting and multiplying that last expression,



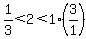or



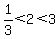and that is true!

Other possible values of x would be ,,, etc. 

How did I get that?

Greater than zero means "positive"
Less than zero means "negative"

We try Case 1:    (which means x is a positive number)



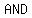
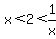We multiply through the right inequality by positive number x
and the inequality sign does not reverse:









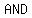
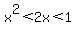
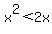
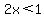
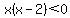
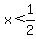Since x is a positive number in this case, and the product
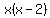 is negative, and since a positive number must 
be multiplied by a negative number in order to get a negative 
number, then 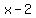 must be a negative number, so





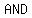
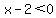
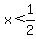
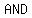
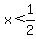In order for a positive number to be both less than 2
and also less than , it needs to be less
than 

So therefore:



We try Case 2:    (which means x is a negative number)



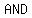
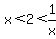If we multiply the second inequality by x, which in this case is 
negative, we reverse the inequality symbols:










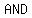
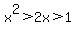
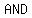
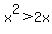
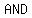
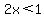
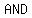
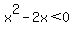
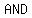
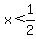
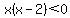
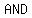
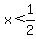Since x is a negative number in this case, and the product
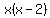 is negative, and since a negative number must 
be multiplied by a positive number in order to get a negative 
number, then 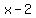 must be a positive number. But then
 implies  with contradicts .

So Case 2 is impossible.

We try Case 3:  x = 0

This is impossible since  would not be defined.

Therefore only Case 1 is possible, so the solution is



and the solution set is 

So x can be any positive value between 0 and , exclusive of
.  x could be any fraction whose numerator is less than half 
its denominator.  Or x could be any decimal whose tenths digit is less \
than 5, such as .437 or .33339, etc.

Edwin