|
Question 309458: a,b, andc can finish a job in 6 days. if b and c work together, the job will take 9 days;if a and c work together, the job will be done in 8 days. in how many days can each man working alone do the job?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! a, b, and c can finish a job in 6 days.
if b and c work together, the job will take 9 days;
if a and c work together, the job will be done in 8 days.
in how many days can each man working alone do the job?
:
Let the completed job = 1
:
"a, b, and c can finish a job in 6 days."
1. + +  + + 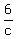 = 1 = 1
:
"if b and c work together, the job will take 9 days;"
2.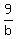 + + 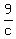 = 1 = 1
:
"if a and c work together, the job will be done in 8 days."
3.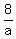 + + 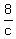 = 1 = 1
:
Multiply eq1 by 3, and eq2 by 2
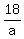 + + 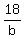 + + 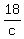 = 3 = 3
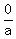 + + 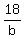 + + 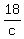 = 2 = 2
--------------------------subtraction eliminates a & b, find c
18/a = 1
Mult both sides by a
a = 18 hrs alone
:
replace a with 18 in eq3, find c
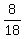 + + 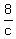 = 1 = 1
Multiply by 18c
8c + 18(8) = 18c
8c + 144 = 18c
144 = 18c - 8c
144 = 10c
c = 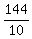
c = 14.4 hrs alone
:
replace c with 14.4 in eq2, find b
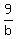 + + 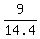 = 1 = 1
multiply by 14.4b
14.4(9) + 9b = 14.4b
129.6 = 14.4b - 9b
129.6 = 5.4b
b = 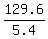
b = 24 hrs alone
:
solution: a=18 hrs, b=24 hrs, c= 14.4 hrs
:
See if that flies in the eq1
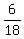 + + 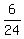 + + 
.333 + .25 + .417 = 1
|
|
|
| |