Question 308992: 4x^2 + ky^2 - 8x + 17y = 3
Find the vaule of k to make this equation a circle, ellipse, hyperbola, and parabola; so different vaules for k that will make those different kinds of equations.
Any single one of them would be helpful if you can't necessairly figure them all out, so if you know anything at all pleaseee help. Thank you so much!
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is very helpful to remember:
For the general conic 
If 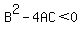 , then the given conic above is an ellipse , then the given conic above is an ellipse
Furthermore, if  , and , and  , then the conic is also a circle , then the conic is also a circle
If  , then the given conic above is a parabola , then the given conic above is a parabola
If 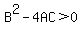 , then the given conic above is a hyperbola , then the given conic above is a hyperbola
First, let's subtract 3 from both sides to get 
So if we wanted to force  to be a circle, then we must make sure that to be a circle, then we must make sure that 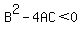 , ,  , and , and  . In this case, . In this case,  , ,  , ,  , ,  , ,  , and , and  . Plug these values in to get . Plug these values in to get 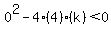 and simplify to get and simplify to get 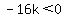 . Solve for 'k' to get . Solve for 'k' to get  . So 'k' must be positive. . So 'k' must be positive.
Also, because we want  and and  , and we know that , and we know that  , this means that , this means that  as well. But as well. But  . So . So 
This means that if  , then we get the circle , then we get the circle 
For any ellipse, just pick a positive 'k' value that is NOT equal to 4. This 'k' value will make 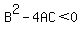 true. true.
For the parabola, just make  since this satisfies the equation since this satisfies the equation  (basically, everything goes to zero since B and C are zero) (basically, everything goes to zero since B and C are zero)
And finally, for any hyperbola, reverse the idea of the ellipse and pick any negative 'k' value. This works because 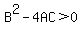 is essentially the opposite of is essentially the opposite of 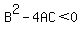
|
|
|