SOLUTION: What type of graph does this equation represent? x^2 + 4y^2 - 2y = 8 THANKS!

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: What type of graph does this equation represent? x^2 + 4y^2 - 2y = 8 THANKS!      Log On


   

Question 308967: What type of graph does this equation represent?
x^2 + 4y^2 - 2y = 8

THANKS!
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2++%2B+4y%5E2+-+2y+=+8 Start with the given equation.


x%5E2++%2B+4%28y%5E2+-+%281%2F2%29y%29+=+8 Factor a 4 from the last two terms on the left side.


x%5E2++%2B+4%28y%5E2+-+%281%2F2%29y%2B1%2F16-1%2F16%29+=+8 Now take half of 1%2F2 to get 1%2F4. Square it to get 1%2F16. Add AND subtract this value inside the parenthesis.


x%5E2++%2B+4%28%28y%5E2+-+%281%2F2%29y%2B1%2F16%29-1%2F16%29+=+8 Group up the first three terms inside the parenthesis.


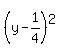
x%5E2++%2B+4%28%28y-1%2F4%29%5E2-1%2F16%29+=+8 Factor that inner group to get %28y-1%2F4%29%5E2


x%5E2++%2B+4%28y-1%2F4%29%5E2-4%281%2F16%29+=+8 Distribute.


x%5E2++%2B+4%28y-1%2F4%29%5E2-4%2F16+=+8 Multiply


x%5E2++%2B+4%28y-1%2F4%29%5E2-1%2F4=+8 Reduce.


x%5E2++%2B+4%28y-1%2F4%29%5E2=+8%2B1%2F4 Add 1%2F4 to both sides.


x%5E2++%2B+4%28y-1%2F4%29%5E2=+33%2F4 Combine like terms.


4x%5E2++%2B+16%28y-1%2F4%29%5E2=+33 Multiply EVERY term (outside the parenthesis) by the LCD 4 to clear out the fraction.


%284x%5E2++%2B+16%28y-1%2F4%29%5E2%29%2F33=+1 Divide both sides by 33 (to make the right side equal to 1).


%284x%5E2%29%2F33++%2B+%2816%28y-1%2F4%29%5E2%29%2F33=+1 Break up the fraction.


%28x%5E2%29%2F%2833%2F4%29++%2B+%28%28y-1%2F4%29%5E2%29%2F%2833%2F16%29=+1 Rearrange the terms in the fractions.


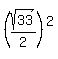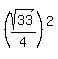
Rewrite 33%2F4 as %28sqrt%2833%29%2F2%29%5E2 and 33%2F16 as %28sqrt%2833%29%2F4%29%5E2


Finally, write x%5E2 as %28x-0%29%5E2


It might be hard to notice, but the last equation above is in the form %28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1 which is an ellipse.


So is an ellipse


This means that x%5E2++%2B+4y%5E2+-+2y+=+8 is also an ellipse (since the two equations are equivalent)


------------------------------------------------------------------------


This is a lot of work to determine the conic. An alternative is to use the following rule:

For the general conic Ax%5E2%2BBxy%2BCy%5E2%2BDx%2BEy%2BF=0

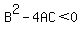If B%5E2-4AC%3C0, then the given conic above is an ellipse
Furthermore, if A=C, and B=0, then the conic is also a circle


If B%5E2-4AC=0, then the given conic above is a parabola


If 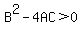B%5E2-4AC%3E0, then the given conic above is a hyperbola


In our case, we have the conic x%5E2++%2B+4y%5E2+-+2y+=+8 which means that A=1, B=0, C=4, D=0, E=-2, and F=-8 (subtract this from both sides). Plug these values into B%5E2-4AC to get 0%5E2-4%281%29%284%29=-16 which is indeed less than 0 meaning that it is an ellipse.


Personally, I recommend doing it the long way for a while at first so you get a feel of what you are doing. Once you understand what's going on, take the shortcut.