Question 30879: Factor completely
2x^2 + 16x + 32
x^3 + 3x^2 + x + 3
3x^2 + 6x - 24
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! 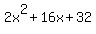
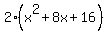
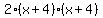
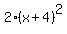
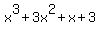
You need to find a factor of this ie a value of x that makes the whole thing zero. Since all the terms are positive, then x must be a negative value, to make the  and x negative. and x negative.
As to the value of x, well this is trial and error to find, but looking at the equation, the value -3 does jump out. Put x=-3 into the expression and you do get zero. So, x+3 is a factor.
You now need to divide this into the cubic expression and then factorise the resulting quadratic, if possible. Having done this for you, the final answer is 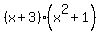 . So try it. . So try it.
Actually, there is a simpler method for this cubic: 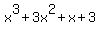 written as written as 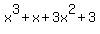 . Look the 2 sets of 2 terms and factorise each of those: . Look the 2 sets of 2 terms and factorise each of those:
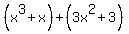
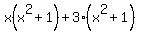
You can see that both halves have 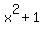 , so we can factorise again, as , so we can factorise again, as 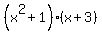
Third example looks to be like the first.
jon.
|
|
|