Question 30563: Solve the problem.
An object is propelled vertically upward rom the top af a112-foot building. the quadratic function s(t) = 16t^2 + 176t + 112 models the ball's height above the ground, s(t), in feet, t seconds after it was thrown. How many seconds does it take until the object finally hits the ground. Round to the nearest tenth of a second if necessary.
Please help me. I am just not getting this. Thank you.
Found 2 solutions by mbarugel, venugopalramana:
Answer by mbarugel(146)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hello!
I think there is a typo in the equation you provided. Note that, if your equation were correct, the height of the object increases continuously as time passes. I'll assume that you actually meant  . Anyway, if the typo was ssomewhere else, you'll be able to follow this reasoning with any equation. . Anyway, if the typo was ssomewhere else, you'll be able to follow this reasoning with any equation.
Note that the equation you provided gives you the height of the object as a function of the time in seconds (t) that passed since it was propelled.
When the object hits the ground, its height is zero. Therefore, we need to find for which 't' this equation is equal to zero. So we get the quadratic equation:

This equation is solved using the standard procedure:
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=38144 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 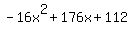 can be factored: can be factored:

Again, the answer is: -0.603277807866851, 11.6032778078669.
Here's your graph:
 |
Clearly, the negative solution (-0.6...) is not relevant. It takes 11.60... seconds for the object to have a height of zero (i.e. hit the ground)
I hope this helps!
Get more answers at Online Math Answers.com!
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! 30563An object is propelled vertically upward rom the top af a112-foot building. the quadratic function s(t) = 16t^2 + 176t + 112 models the ball's height above the ground, s(t), in feet, t seconds after it was thrown. How many seconds does it take until the object finally hits the ground. Round to the nearest tenth of a second if necessary.
THERE IS NOTING AMISS IN YOU NOT GETTING THE SOLUTION IF YOU ARE NOT TAUGHT CALCULUS...WE CAN CIRCUMVENT THAT BY USING SOME CIRCUTOUS PROCEDURE.BUT YOU TELL ME FIRST WHETHER YOU KNOW DIFFERENTIATION...SEE BELOW.
FURTHER I FEEL THE FORMULA IS BETTER REPRESENTED BY S= -16T^2+176T+112.(YOU WILL FIND THAT THIS ELIMINATES NEGATIVE TIMINGS OBTAINED BELOW.)
WE HAVE TO CONSIDER 2 MOTIONS HERE.
1.UPWARD...THE OBJECT GOES UP TILL ITS VELOCITY BECOMES ZERO.LET IT GO A DISTANCE H DURING THIS PART.
2.DOWNWARD.....THE OBJECT FALLS ON TO THE GROUND.DURING THIS PHASE IT HAS TO TRAVEL H..THE SAME DISTANCE IT HAS GONE UP PLUS 112 FT THE HEIGHT OF THE BUILDING...SO DISTANCE TRAVELLED DURING DESCENT =H+112
3.HENCE TOTAL DISTANCE TRAVELLED IS H+H+112=2H+112
s(t) = 16t^2 + 176t + 112
VELOCITY =DS/DT =32T+176
WHEN THE OBJECT REACHES ITS TOP POSITION ,ITS VELOCITY BECOMES ZERO AND IT STARTS TO FALL DOWN
HENCE TIME TAKEN TO REACH PEAK IS GIVEN BY VELOCITY = 0 = 32T+176
T=176/32= - 5.5 ůMINUS IS BECAUSE ,THE GIVEN FORMULA DOES NOT DISTINGUISH FOR UPWARD/DOWNWARD MOTION.WE CAN TAKE ABSOLUTE VALUE FOR OUR PURPOSE. IT TAKES SAME TIME FOR DECENT UPTO TOP OF BUILDING.HENCE
TIME FOR DOWNWARD MOVEMENT UPTO TOP OF BUILDING = 5.5
DISTANCE FROM TOP OF BUILDING TO GROUND = 112.SO TIME FOR THIS TRAVEL IS GIVEN BY....S=112 = 16T^2+176T+112
16T(T+11)=0..HENCE T+11=0....OR T= -11
SO TOTAL TIME TAKEN IS = 5.5+5.5+11 = 22...
NOW ON TO SOLUTION WITHOUT CALCULUS...THAT IS SOLVING FOR TIME TAKEN TO REACH THE PEAK FROM BUILDING TOP AND COMING BACK TO TOP OF BUILDING WITHOUT DIFFERENTIATION TO GET AT VELOCITY.
YOU CAN TREAT THE GIVEN EQN.AS A QUADRATIC WITH A PEAK REPRESENTING THE TOP POSITION OF OBJECT AS EXPLAINED ABOVE.THIS HELPS TO GET THE TIME TAKEN TO REACH THE PEAK AS A PHYSICAL INTERPRETATION OF THE FORMULA/PHENOMENA.
S=16T^2+176T+112=16{T^2+11T+7)=16{(T^2+2T(11/2)+(11/2)^2)-(11/2)^2+7)}
=16{(T+5.5)^2-93/4}....SO THE PEAK OCCURS AT
T+5.5=0..OR...T=-5.5...THE NEGATIVE SIGN WAS ALREADY EXPLAINED ABOVE...
THUS YOU CAN SHOW T=5.5 FOR ASCENT +5.5 FOR DESCENT.FURTHER TRAVEL BY S=112 FROM TOP OF BUILDING CAN BE DONE BY SAME WAY AS ABOVE AS IT DOES NOT INVOLVE ANY CALCULUS.
|
|
|