Question 305478: I'm not sure if this is too big a question but if someone could at least point me in the right direction I'd appriciate it.
Place 3 circles with the same radius, r, with their centers on a horizontal in such a way that the middle circle intersects the left and right circles in exactly 1 point each(like 3 coins, touching, all in a row). Draw a line from the center of the left circle that is tangent to the right circle. This line intersects the middle circle in 2 points. Find the length of the line segment connecting these 2 points in terms of r.
Ok so I have the picture fine I'm pretty sure about that. In the middle circle i tried drawing radii from the center to the points of the segment i have to find the length of, and i know it's an isosceles triangle but that doesn't help me find the length of that segment. I've also tried right triangles in different areas but nothing i have come up with has helped...once again I'd really appriciate it if someone could at least steer me in the right direction. Thanks!
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! Make the origin the center of your first circle (left hand side).
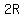The center of the middle circle is then ( , ) and the equation of the middle circle is then,
The tangent line also starts at (,) and has has the formula,
The tangent line is the base of a right triangle that has a hypotenuse equal to  and the other side  . The third side is then, by the Pythagorean theorem,
The tangent of the angle that the tangent line makes with the x-axis is then equal to opposite side, , over the adjacent side,  . This is also the slope you need "m".
You can then plug that into your circle equation to find the two intersection points.
.
.
.
Once you have the points, you can use the distance formula to calculate the distance between the points.
|
|
|
