Question 304976: If x is a negative number, which of the following must be true?
I) x^5 < |x|
II) x < √(-x)
III) x - 1/|x| < 0
A) I, II and III
B) I and II only
C) None
D) II and III only
E) I and III only
Found 2 solutions by Edwin McCravy, Theo:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
I) x5 < |x|
That's always true because x5 is negative if x is negative,
and |x| is always positive if x is is negative.
____
II) x < √(-x)
That's always true because if x is negative,
the left side is negative and the right side positive.
III) x - 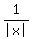 < 0
That is always true because subtracting a positive from
a negative also gives a negative which is less than 0.
A) I, II and III
That's the only correct answer.
Edwin
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! The best way to determine this is to use examples.
The first statement says that x^5 is smaller than the absolute value of x, shown as |x|.
This has to be true because x^5 is always a negative number and a negative number is always less than a positive number.
For example:
If x = -2, then x^5 = -32 which is smaller than 2.
If x = -1, then x^5 = -1 which is smaller than 1.
If x = -.2, then x^5 = -.00032 which is smaller than .2
You can't find a negative number that when raised to the 5th power is greater than or equal to a positive number, so this has to be a true statement for all negative numbers.
The second statement says that x is smaller than the square root of -x.
If x is negative, than -x is positive and the square root of -x is equal to plus or minus the square root of a positive number.
If you let x = -25, then:
Plus square root of 25 is equal to 5. Since -25 is less than or equal to 5, this has to be true.
Minus square root of 25 is equal to -5. Since -25 is less than or equal to -5, this also has to be true.
If you let x = -1, then:
Plus square root of 1 is equal to 1. Since -1 is less than or equal to 1, this has to be true.
Minus square root of 1 is equal to -1. Since -1 is NOT less than or equal to -01, this has to be false.
If you let x = -.25, then:
Plus square root of .25 is equal to .5. Since -.25 is less than or equal to .5, this has to be true.
Minus square root of .25 is equal to -.5. Since -.25 is NOT less than -.5, this has to be false.
Since you found at least one instance where a negative number is NOT less than the square root of minus the negative number, then this statement is false.
The third statement says that a negative number minus (1 divided by the absolute value of the negative number) is always less than 0.
If your number is -5, then 1/5 = .2 and -5 - .2 = -5.2. Since -5.2 is less than 0, then this statement is true.
If your number is -1, then 1/1 = 1 and -1 - 1 = -2. Since -2 is less than 0, then this statement is true.
If your number is -.5, then 1/.5 = 2 and -.5 - 2 = -2.5. Since -2.5 is less than 0, then this statement is true.
Since you can't find a negative number where this statement is false, then this statement is always true.
Your answer appears to be selection E (I and III only).
You could not really generalize these statements to prove them true or not.
You had to find examples and test them out.
The dividing line appears to be 1.
You had to test number whose absolute value of greater than 1, equal to 1, and less than 1.
Only testing with numbers greater than 1 would have led to a bad conclusion.
I almost did that with statement II until I tested with number whose absolute value was equal to 1 and less than 1.
|
|
|
