Question 302070: A rectangle is 3 times as long as it is wide and has the same perimeter as a square whose area is 4 square feet larger than that of the rectangle. What are the dimensions of both the rectangle and the square?
Found 2 solutions by mananth, MathTherapy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! A rectangle is 3 times as long as it is wide and has the same perimeter as a square whose area is 4 square feet larger than that of the rectangle. What are the dimensions of both the rectangle and the square?
let the width be x
the length will be 3x
the perimeter of rectangle = 2*x+2*3x =8x
Area of aquare = 4 sq.feet
so length =2 feet
the permeterof square = 4*2 =8
perimeter of rectangle = permeter of square
8x = 8
x=1 which is the width
length =3x
so length = 3 feet
Ananth
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website! A rectangle is 3 times as long as it is wide and has the same perimeter as a square whose area is 4 square feet larger than that of the rectangle. What are the dimensions of both the rectangle and the square?
Let rectangle’s width = W
Then rectangle’s length or L = 3W. Its perimeter = 2W + 2(3W) or 8W, and its area =  .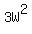
Square’s perimeter = 8W, since its perimeter is same as that of the rectangle, which makes one of its sides 2W, and its area  .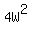
Since square’s area is 4 sq ft larger than that of the rectangle, then  , or,  , which means that:
W, or width of rectangle =  , and its length  (2*3).
This also makes one side of the square 2W, or  (2*2)
|
|
|
