Question 301235: In 2005, consumers received, on average, 3253 spam
messages. The volume of spam messages per consumer
is decreasing exponentially with an exponential
decay rate of 13.7% per year.
a) Find the exponential decay function that can be
used to predict the average number of spam messages,
, t years after 2005.
b) Predict the number of spam messages received
per consumer in 2010.
c) In what year, theoretically, will the average consumer
receive 100 spam messages?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In 2005, consumers received, on average, 3253 spam messages.
The volume of spam messages per consumer is decreasing exponentially with an
exponential decay rate of 13.7% per year.
:
a) Find the exponential decay function that can be used to predict the average
number of spam messages, t years after 2005.
The equation:
S = 3253(1-.137)^t
S = 3253(.863)^t
:
b) Predict the number of spam messages received per consumer in 2010.
t=5
S = 3253(.863)^5
S = 1557 spam msg in 2010
c) In what year, theoretically, will the average consumer receive 100 spam messages?
S = 100:
3253(.863)^t = 100
(.863)^t = 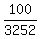
.863^t = .03074
t*log(.863) = log(.03074
t = 
t = 23.6 ~ 24 yrs
:
2005 + 24 = 2029 yr when spam msg down to 100
:
:
Check solution in a calc: enter 3253(.863)^23.6 = 100.5, close enough
|
|
|