Question 30099: an extra credit for my honors math class. i cant figure it out for the life of me...
derive the formula A=Pe^rt from the general formula for compounding interestL A=P(1+r/n)^n*t
Answer by Fermat(136)   (Show Source): (Show Source):
You can put this solution on YOUR website!  - interest compounded periodically - interest compounded periodically
 ------- interest compounded continuously ------- interest compounded continuously
When interest is compounded continously, this means letting the number of periods in a year increase without bound.
In other words, we find the limit, as n tends to infinity of 
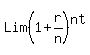
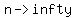
Binomial theorem

Applying the Binomial theorem to 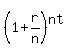 , we get , we get


as 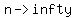 , , 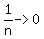 , giving , giving
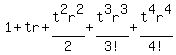

and the above is the Maclaurin series for 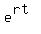
i.e. 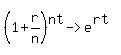 as as 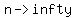
We wanted to find the limit, as n tends to infinity of  and we have the limit, as n tends to infinity, of and we have the limit, as n tends to infinity, of 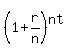 which is which is 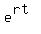 . We substitute . We substitute 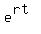 for for  . .
So for continuous compounding we can write,

==========
|
|
|