|
Question 299505: find the vertices, center, and foci of the ellipse, and sketc its graph 9x^2+4y^2-36x+8y+31=0
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the vertices, center, and foci of the ellipse, and sketc its graph 9x^2+4y^2-36x+8y+31=0
Rearrange
 Factor out coefficients of squared letters:
Factor out coefficients of squared letters:
 Complete the square in the first parentheses by
adding
Complete the square in the first parentheses by
adding  inside the first parentheses
which actually amounts to adding 36 to the left side
because there is a 9 in front of the parentheses, so
we must add a 36 to the right side: inside the first parentheses
which actually amounts to adding 36 to the left side
because there is a 9 in front of the parentheses, so
we must add a 36 to the right side:
 Complete the square in the second parentheses by
adding
Complete the square in the second parentheses by
adding 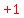 inside the second parentheses
which actually amounts to adding 4 to the left side
because there is a 4 in front of the parentheses, so
we must add a 4 to the right side: inside the second parentheses
which actually amounts to adding 4 to the left side
because there is a 4 in front of the parentheses, so
we must add a 4 to the right side:
 Factoring the parentheses as a perfect squares:
Factoring the parentheses as a perfect squares:
 Get a 1 on the right by dividing through by 9
Get a 1 on the right by dividing through by 9

 To get the 4 off the top of the second fraction we
divide top and bottom by 4:
To get the 4 off the top of the second fraction we
divide top and bottom by 4:


 Since the largest denominator is under the term in
y, the ellipse has a vertical major axis. So we
compare it to:
Since the largest denominator is under the term in
y, the ellipse has a vertical major axis. So we
compare it to:

 , ,  , ,
 so so 
 so so  Its center is at (h,k) = (1,
Its center is at (h,k) = (1, Draw the major axis
Draw the major axis  units both above and below the center.
Draw the minor axis units both above and below the center.
Draw the minor axis  units both right and left of the center. units both right and left of the center.
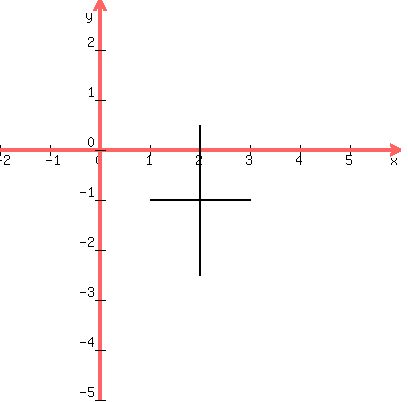 The vertices are
The vertices are  units above and below the center (2,-1)
So we add units above and below the center (2,-1)
So we add  to the y-coordinate of the center to the y-coordinate of the center
 so the upper vertex is (2, so the upper vertex is (2, )
And we subtract )
And we subtract  from the y-coordinate of the center from the y-coordinate of the center
 so the lower vertex is (2, so the lower vertex is (2, )
Sketch in the ellipse: )
Sketch in the ellipse:
 To find the foci, we must calculate c, using the Pythagorean
relationship
To find the foci, we must calculate c, using the Pythagorean
relationship





 The foci are
The foci are  units above and below the center (2,-1)
So we add units above and below the center (2,-1)
So we add  to the y-coordinate of the center to the y-coordinate of the center
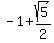 so the upper vertex is (2, so the upper vertex is (2,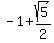 )
And we subtract )
And we subtract  from the y-coordinate of the center from the y-coordinate of the center
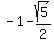 so the upper vertex is (2, so the upper vertex is (2,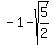 )
They are approximately
(1,0.12) and (1,-2.12)
We draw them in )
They are approximately
(1,0.12) and (1,-2.12)
We draw them in
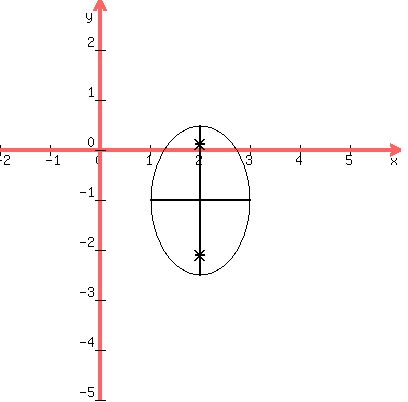 Edwin
Edwin
|
|
|
| |