Question 299180: Please express as a single logarithm:
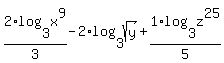
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Basic concepts you will use:



 (exponent is (exponent is 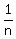 ) )

Start with each term separately.
Your expression is:
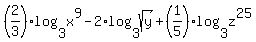
First term becomes:
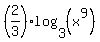 = = 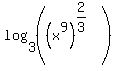 = = 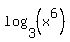
Second term becomes:
 = =  = =  = = 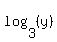
Third term becomes:
 = =  = = 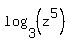
Putting all 3 terms together, your expression becoms:
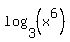 - - 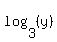 + + 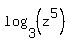
Since  , then your expression becomes: , then your expression becomes:

You can confirm the final expression is equivalent to the original expression by taking any values of x, y, and z and substituting in both the original expression and the final expression.
If you come up with the same answer, you did good.l
I confirmed with x = 3, y = 4, and z = 5.
I used 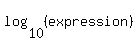 rather than rather than 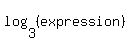 because the calculator can solve logs to the base of 10 more easily. because the calculator can solve logs to the base of 10 more easily.
That shouldn't matter since the expressions should work with any base as long as all bases in the expression are the same.
Just to make sure, I solved with  as well. as well.
Both confirmed that the answer with the original expression was the same as the answer with the final expression.
When you solve an expression to the base of anything other than 10 using the calculator, you simply take the take the log of the expression to the base of 10 and then divide that answer by the log of the other base to the base of 10.
An example will show you how that's done.
You know that  = 32 because you can use your calculator to confirm that. = 32 because you can use your calculator to confirm that.
This means the 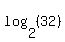 = 5 because that's the way logs work. = 5 because that's the way logs work.
By definition, 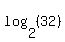 = 5 if and only if = 5 if and only if  = 32. = 32.
You can't solve that log directly using your calculator, but you can solve the log using the base conversion formula.
You get:
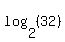 = = 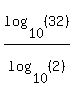 = 5 = 5
|
|
|