SOLUTION: The sum of the first 100 terms of the sequence 1, -2, 3, 4, -5, 6, 7, -8, 9, 10… is 1750. The sum of the first 100 terms of the sequence 1, 2, -3, 4, 5, -6, 7, 8, -9, 10… is equal

Let the answer be x.

1, -2, 3, 4, -5, 6, 7, -8, 9, 10…

The signs go in groups of three +, -,  +,  so the last group of three
less than 100 that have signs like that will end in a multiple of 3,
which is the group +97, -98, +99, since 99 is the largest multiple of 99.
The last term would be +100 because 100 would be the beginning of the next 
group of three that go +, -, +, so we have:

1 - 2 + 3 + 4 - 5 + 6 + 7 - 8 + 9 + 10 + … + 97 - 98 + 99 +100 = 1750.

Next we look at the second sequence:

1, 2, -3, 4, 5, -6, 7, 8, -9, 10…

The signs also go in groups of three +, +,  -,  so the last group of three
less than 100 that have signs like that are +97, +98, -99, so the last
term would be +100 because it would be the beginning of the next group
of three that go +, +, -, so we have:

1 + 2 - 3 + 4 + 5 - 6 + 7 + 8 - 9 + 10 + … + 97 + 98 - 99 + 100 = x.

Now let's add the two sequences together term by term:

1 - 2 + 3 + 4 - 5 + 6 +  7 - 8 + 9 + 10 + … +  97 - 98 + 99 + 100 =   1750  
1 + 2 - 3 + 4 + 5 - 6 +  7 + 8 - 9 + 10 + … +  97 + 98 - 99 + 100 =      x
---------------------------------------------------------------------------
2 + 0 + 0 + 8 + 0 + 0 + 14 + 0 + 0 + 20 + … + 194 +  0 +  0 + 200 = 1750+x

The left side is the arithmetic sequence with  and  

2 + 8 + 14 + 20 + ... + 194 + 200

To find the number of terms, n, we can do it by observing the
groups of 3, but if you can't tell there would be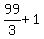  
or 34 terms, then we can calculate the n=34 this way:







So





Therefore the equation

2 + 0 + 0 + 8 + 0 + 0 + 14 + 0 + 0 + 20 + … + 194 +  0 +  0 + 200 = 1750+x

becomes




and the required sum is 1684.

Edwin