Question 297613: How do I calculate all the possible rectangles that can fit into a 2D rectangle?
For instance if the large rectangle has height H = 2 and width W = 5 the total number of rectangles that can fit into it are 31.
what formula do I use to find all rectangles (including the large rectangle)that can fit into H x W? I tried dividing the rectangle by smaller values of H and W increasing, but still didn't get the right answer. Please help
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! For a  and and  rectangle, you get rectangle, you get
10  , , rectangles rectangles
8  , ,  rectangles rectangles
6  , ,  rectangles rectangles
4  , ,  rectangles rectangles
2  , ,  rectangles rectangles
5  , ,  rectangles rectangles
4  , ,  rectangles rectangles
3  , ,  rectangles rectangles
2  , ,  rectangles rectangles
1  , ,  rectangles rectangles
That's a total of  rectangles. rectangles.
.
.
.
Now for a formula.
Start simple and work up to see a pattern.
 , , 


 total rectangles total rectangles
.
.
.
 , , 




 total rectangles. total rectangles.
.
.
 , , 






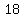 total total
.
.
.
 , , 








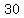 total rectangles. total rectangles.
.
.
You're starting to get a pattern.
The 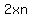 rectangles sum from rectangles sum from  to to  in steps of in steps of  for a total of for a total of 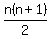 . .
The 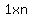 rectangles sum for rectangles sum for  to to  in steps of in steps of  or or 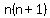 . .
So the grand total of rectangles in a 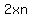 rectangle would be rectangle would be


|
|
|