Question 295272: Exactly 100 people live in a village. The oldest person in the village was born in 1900 and everybody in the village was born in a different year but all on January 1st. In 1999, the sum of the digits in Julie's birth year was equal to her age. How old was she?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Exactly 100 people live in a village. The oldest person in the village was born in 1900 and everybody in the village was born in a different year but all on January 1st. In 1999, the sum of the digits in Julie's birth year was equal to her age. How old was she?
Suppose Julie's was born in the year "19tu", then the last
two digits of her birth year is 10t+u, and her age in
1999 was therefore 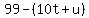 . .
The sum of the digits of her birth year is 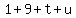
Since her age = the sum of the digits of her birth year, then



The least coefficient in absolute value is 2, so
we write all other integers in that equation in terms of
their nearest multiple of 2:


We divide through by 2:


Isolate the fractions on the right:

Since the left side is an integer, the right side is too.
Let that integer be A. So both sides = A:
 . .
Clear the first equation of fractions:


Substituting in





u is a digit, so

Substituting 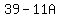 for u for u




Since A is an integer it can only be 3,
for 3 is the only integer in that interval.
So 








Therefore she was born in 1976 and therefore in 1999, she was 23,
and indeed the sum of the digits of her birth year is 1+9+7+6=23,
which is her age.
Edwin
|
|
|