|
Question 29439: x^2+x<12
Found 3 solutions by Bb, amalm06, ikleyn:
Answer by Bb(20)   (Show Source): (Show Source):
You can put this solution on YOUR website! ok 1st u simplify the problem 2x^2<12=4x<12 then u divide by 4 on each side and u get x<4 to chek u replace the x with 3 so u get 3^2+3<12
i hope that helps
Answer by amalm06(224)   (Show Source): (Show Source):
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
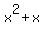 < 12. (1)
Subtract 12 from both sides. You will get an EQUIVALENT inequality < 12. (1)
Subtract 12 from both sides. You will get an EQUIVALENT inequality
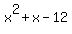 < 0. (2)
It is the same as to move the term 12 in the original equation from the right side
to its left side changing the sign.
In the inequality (2), factor left side. You will get an EQUIVALENT inequality
(x+4)*(x-3) < 0. (3)
You have quadratic function in the left side.
This quadratic function is ZERO at x= -4 and at x=3.
It is POSITIVE at x < -4, NEGATIVE in the interval -4 < x < 3, and POSITIVE again in the interval x > 3.
So, the solution to your original inequality is the set of all real numbers
-4 < x < 3, or, in interval notation (-4,3).
To check, take the number x = -3, for example, and calculate the quadratic function (1):
(-3)^2 + (-3) = 9 - 3 = 6. It is less than 12, so it is correct.
Answer. The solution to your original inequality is the set of all real numbers -4 < x < 3, or, in interval notation, the interval (-4,3). < 0. (2)
It is the same as to move the term 12 in the original equation from the right side
to its left side changing the sign.
In the inequality (2), factor left side. You will get an EQUIVALENT inequality
(x+4)*(x-3) < 0. (3)
You have quadratic function in the left side.
This quadratic function is ZERO at x= -4 and at x=3.
It is POSITIVE at x < -4, NEGATIVE in the interval -4 < x < 3, and POSITIVE again in the interval x > 3.
So, the solution to your original inequality is the set of all real numbers
-4 < x < 3, or, in interval notation (-4,3).
To check, take the number x = -3, for example, and calculate the quadratic function (1):
(-3)^2 + (-3) = 9 - 3 = 6. It is less than 12, so it is correct.
Answer. The solution to your original inequality is the set of all real numbers -4 < x < 3, or, in interval notation, the interval (-4,3).
The solution by @amalm06 is TOTALLY WRONG.
Below please see the plot to your inequality.

Plot y = 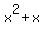 (red) and y = 12 (green) (red) and y = 12 (green)
You are searching for those x where the parabola is BELOW the horizontal green line.
|
|
|
| |