If 3 dice are rolled at the same time, what is the probability of all 3 dice showing even face
values? (i.e. all 3 dice showing 2, 4, or 6)
We calculate the numerator of the desired probability:
There are 3 ways an even number can show up on the first die
AND
There are 3 ways an even number can show up on the second die
AND
There are 3 ways an even number can show up on the third die
So since "AND" means "MULTIPLY", there are 3x3x3 or 27 ways
the three dice can all come up even. So the numerator of
the probability is 27.
We calculate the denominator of the desired probability:
There are 6 ways any number can show up on the first die
AND
There are 6 ways any number can show up on the second die
AND
There are 6 ways any number can show up on the third die
So since "AND" means "MULTIPLY", there are 6x6x6 or 216 ways
the three dice can all come up any number. So the denominator
of the probability is 216.
Therefore the desired probability is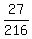 
or 
Below is the sample space of all 216 outcomes, and the 27 red
ones are the successful outcomes.
(1,1,1) (1,1,2) (1,1,3) (1,1,4) (1,1,5) (1,1,6)
(1,2,1) (1,2,2) (1,2,3) (1,2,4) (1,2,5) (1,2,6)
(1,3,1) (1,3,2) (1,3,3) (1,3,4) (1,3,5) (1,3,6)
(1,4,1) (1,4,2) (1,4,3) (1,4,4) (1,4,5) (1,4,6)
(1,5,1) (1,5,2) (1,5,3) (1,5,4) (1,5,5) (1,5,6)
(1,6,1) (1,6,2) (1,6,3) (1,6,4) (1,6,5) (1,6,6)
(2,1,1) (2,1,2) (2,1,3) (2,1,4) (2,1,5) (2,1,6)
(2,2,1) (2,2,2) (2,2,3) (2,2,4) (2,2,5) (2,2,6)
(2,3,1) (2,3,2) (2,3,3) (2,3,4) (2,3,5) (2,3,6)
(2,4,1) (2,4,2) (2,4,3) (2,4,4) (2,4,5) (2,4,6)
(2,5,1) (2,5,2) (2,5,3) (2,5,4) (2,5,5) (2,5,6)
(2,6,1) (2,6,2) (2,6,3) (2,6,4) (2,6,5) (2,6,6)
(3,1,1) (3,1,2) (3,1,3) (3,1,4) (3,1,5) (3,1,6)
(3,2,1) (3,2,2) (3,2,3) (3,2,4) (3,2,5) (3,2,6)
(3,3,1) (3,3,2) (3,3,3) (3,3,4) (3,3,5) (3,3,6)
(3,4,1) (3,4,2) (3,4,3) (3,4,4) (3,4,5) (3,4,6)
(3,5,1) (3,5,2) (3,5,3) (3,5,4) (3,5,5) (3,5,6)
(3,6,1) (3,6,2) (3,6,3) (3,6,4) (3,6,5) (3,6,6)
(4,1,1) (4,1,2) (4,1,3) (4,1,4) (4,1,5) (4,1,6)
(4,2,1) (4,2,2) (4,2,3) (4,2,4) (4,2,5) (4,2,6)
(4,3,1) (4,3,2) (4,3,3) (4,3,4) (4,3,5) (4,3,6)
(4,4,1) (4,4,2) (4,4,3) (4,4,4) (4,4,5) (4,4,6)
(4,5,1) (4,5,2) (4,5,3) (4,5,4) (4,5,5) (4,5,6)
(4,6,1) (4,6,2) (4,6,3) (4,6,4) (4,6,5) (4,6,6)
(5,1,1) (5,1,2) (5,1,3) (5,1,4) (5,1,5) (5,1,6)
(5,2,1) (5,2,2) (5,2,3) (5,2,4) (5,2,5) (5,2,6)
(5,3,1) (5,3,2) (5,3,3) (5,3,4) (5,3,5) (5,3,6)
(5,4,1) (5,4,2) (5,4,3) (5,4,4) (5,4,5) (5,4,6)
(5,5,1) (5,5,2) (5,5,3) (5,5,4) (5,5,5) (5,5,6)
(5,6,1) (5,6,2) (5,6,3) (5,6,4) (5,6,5) (5,6,6)
(6,1,1) (6,1,2) (6,1,3) (6,1,4) (6,1,5) (6,1,6)
(6,2,1) (6,2,2) (6,2,3) (6,2,4) (6,2,5) (6,2,6)
(6,3,1) (6,3,2) (6,3,3) (6,3,4) (6,3,5) (6,3,6)
(6,4,1) (6,4,2) (6,4,3) (6,4,4) (6,4,5) (6,4,6)
(6,5,1) (6,5,2) (6,5,3) (6,5,4) (6,5,5) (6,5,6)
(6,6,1) (6,6,2) (6,6,3) (6,6,4) (6,6,5) (6,6,6)
------------------------------
If 2 dice are rolled at the same time, what is the probability of the 2 dice having the same face value?
We calculate the numerator of the desired probability:
There are 6 ways any number can show up on the first die
AND
There is only 1 way that same number can show up on the second die
So since "AND" means "MULTIPLY", there are 6x1 or 6 ways
that both dice can come up the same. So the numerator of
the probability is 6.
We calculate the denominator of the desired probability:
There are 6 ways any number can show up on the first die
AND
There are 6 ways any number can show up on the second die
So since "AND" means "MULTIPLY", there are 6x6 or 36 ways
the two dice can all come up any number. So the denominator
of the probability is 36.
Therefore the desired probability is 
or 
Below is the sample space of all 36 outcomes, and the 6 red
ones are the successful outcomes.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Edwin
