|
Question 293503: For each equation, state the x-intercept and y-intercept. Then graph the equation using the intercepts and a third point.
Helen's Health Foods usually sells 400 cans of ProPac Punch per week when the price is $5 per can. After experimenting with prices for some time. Helen has determined that the weekly demand can be found by using the equation d=600-40p, where d is te number of cans and p is the price per can.
a)Will Helen sell more or less Muscle Punch if she raises her price from $5?
b)What happens to her sales every time she raises her price by $1?
c)Graph the equation.
d)What is the maximum price that she can charge and still sell at least one can?
Can you please help me with this problem? thank you
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! d = 600 - 40p
d is the number of cans
p is the price per can
When p = 5, d = 600 - 40*5 = 600 - 200 = 400 cans per week.
When p = 6, d = 600 - 40*6 = 600 - 240 = 360 cans per week.
When p = 7, d = 600 - 40*7 = 600 - 280 = 320 cans per week.
Every dollar increase in the price means 40 less cans sold per week.
Your questions are:
-----
a)Will Helen sell more or less Muscle Punch if she raises her price from $5?
She will sell less punch.
-----
b)What happens to her sales every time she raises her price by $1?
She sells 40 less cans per week.
-----
c)Graph the equation.
To graph this equation, change d to y and change p to x.
Your equation becomes y = 600 - 40*x
Graph of your equation looks like this:
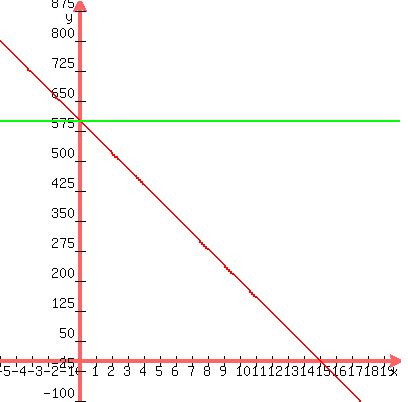
-----
d)What is the maximum price that she can charge and still sell at least one can?
From the graph, it's clear that when she sells at $15.00 per can, she will not sell any cans.
From the formula, this becomes d = 600 - 40*15 = 600 - 600 = 0
As long as the price is less than $15.00 per can, she will sell something, even if it's just part of a can.
Since she can't really sell part of a can, the smallest increment she can sell is 1 can.
We can figure out what the highest price has to be in order for her to sell 1 can.
The formula is:
d = 600 - 40*p
We set d = 1 to get:
1 = 600 - 40*p
We subtract 1 from both sides of this equation and we add 40*p to both sides of this equation to get:
40*p = 599
We divide both sides of this equation by 40 to get:
p = 599/40 = $14.975 per can.
At that price, she will sell 1 can.
That's the highest price she can sell each can for and still be able to sell at least 1 can based on the formula.
Her price must be less than or equal to $14.975 in order for her to sell at least 1 can.
That's the answer to question d.
The rest is just additional information.
Continue reading only if interested.
It appears that the differential price per can is equal to $15.00 - $14.975 = $.025.
This means that if she drops the price by another $.025, she should be able to sell exactly 1 more can.
To see if that works, we put that into the formula.
The formula is d = 600 - 40*p
We set p = $14.975 and we get d = 600 - 40*14.975 = 600 - 599 = 1
We set p = $14.950 and we get d = 600 - 40*14.950 = 600 - 598 = 2
The increment for selling exactly 1 more or less cans is equal to $.025 per can.
That makes sense because in the formula d = 600 - 40*p, if we just look at the 40*p part, we see that 40*.025 = 1, 40*.05 = 2, etc.
Your answer to question d is that the maximum price per can in order for her to sell at least 1 can is $14.975 per can.
|
|
|
| |