A fair coin is tossed until first tail comes up. Let A be the event that the number of tosses is divisible by 5,
Find P(A)
The other tutor's solution is incorrect.
P(A) = P(x=5 or x=10 or x=15 or ... x=5n or ...)
Since "or" implies "add"
P(A) = P(x=5) + P(x=10) + P(x=15) + ... + P(x=5n) + ...
P(x=5) = 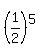 , which means the 5 tosses went HHHHT
P(x=10) =
, which means the 5 tosses went HHHHT
P(x=10) = 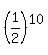 which means the 10 tosses went HHHHHHHHHT
P(x=15) =
which means the 10 tosses went HHHHHHHHHT
P(x=15) = 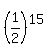 which means the 15 tosses went HHHHHHHHHHHHHHT
...
P(x=5n) =
which means the 15 tosses went HHHHHHHHHHHHHHT
...
P(x=5n) = 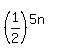 ...
P(A) = the sum of an infinite geometric series with
...
P(A) = the sum of an infinite geometric series with  and
and 
 ------------------------
------------------------
Let B be the event that the number of tosses is less than 6
Find P(B)
P(B) = P(T or HT or HHT or HHHT or HHHHT or HHHHT) =
Since "or" implies "add"
P(B) = P(T) + P(HT) + P(HHT) + P(HHHT) + P(HHHHT) =
P(B) = 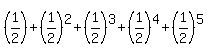 P(B) =
P(B) =  ---------------------
---------------------
Find P(AuB)
Use the formula:
P(A U B) = P(A or B) = P(A) + P(B) - P(A and B)
We have P(A) = 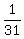 , P(B) =
, P(B) = 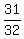 The event "A and B" is the event HHHHT, the only event
which would be both a multiple of 5 tosses and also less
than 6 tosses.
HHHHT has probability
The event "A and B" is the event HHHHT, the only event
which would be both a multiple of 5 tosses and also less
than 6 tosses.
HHHHT has probability  =P(A and B)
P(A U B) = P(A or B) = P(A) + P(B) - P(A and B)
P(A U B) = P(A or B) =
=P(A and B)
P(A U B) = P(A or B) = P(A) + P(B) - P(A and B)
P(A U B) = P(A or B) =  Edwin
Edwin