SOLUTION: the directions say to put the following equation into graphing form... i dont know how to do the squared sign on a key board so 2x2 is two x squared 2x2 + 3y2 + 4x - 12y -4 = 0

Rearrange



Factor out coefficients of squared letters:



Complete the square in the first parentheses by
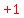adding  inside the first parentheses
which actually amounts to adding 2 to the left side 
because there is a 2 in front of the parentheses, so
we must add a 2 to the right side:



Complete the square in the second parentheses by
adding  inside the second parentheses
which actually amounts to adding 12 to the left side 
because there is a 3 in front of the parentheses, so
we must add a 12 to the right side:



Factoring the parentheses as perfect squares:



Get a 1 on the right by dividing through by 18





Since the largest denominator is under the term in
x, the ellipse has a horizontal major axis.  So we
compare it to:



, , 

 so 

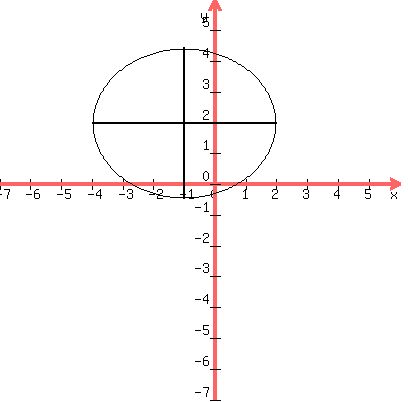
 so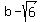 

Its center is at (h,k) = (-1,2)

Plot the center:


 
Draw the major axis  units both right and left of the center.
Draw the minor axis  units up and down
from the center.


Connect them to show the major and minor axes
of the ellipse:
 

 
Sketch in the ellipse:
 


 
Edwin