SOLUTION: I am a regular polygon with all obtuse angles. i have the smallest number of sides of any polygon with obtuse angles. how many sides do i have?

Algebra ->  Polygons -> SOLUTION: I am a regular polygon with all obtuse angles. i have the smallest number of sides of any polygon with obtuse angles. how many sides do i have?      Log On


   

Question 290917: I am a regular polygon with all obtuse angles. i have the smallest number of sides of any polygon with obtuse angles.
how many sides do i have?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

The fotmula for the sum of the interior angles of
any n-sided polygon is (n-2)*180°, and since
a regular polygon has n congruent interior angles,
each one has %28%28n-2%29%2A%22180%B0%22%29%2Fn

You can't have 3 sides because a regular 3-sided polygon is an
equilateral triangle, which has 60° interior angles.



You can't have 4 sides because a regular 4-sided polygon is a
square, which has 90° interior angles.

drawing%28200%2C200%2C-1.5%2C1.5%2C-1%2C2%2Crectangle%28-1%2C-.5%2C1%2C1.5%29+%29

So you must have 5 sides because a regular pentagon has
108° interior angles, and a 108° angle is an obtuse angle.  



Maybe your teacher wants you to do it this way:

Since an obtuse angle is one greater than 90°
You could get the answer by the inequality

%28%28n-2%29%2A%22180%B0%22%29%2Fn%3E%2290%B0%22

Multiply through by n.  Since n is positive,
we do not reverse the inequality:

%28n-2%29%2A180%3E90n

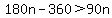
180n-360%3E90n

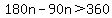
180n-90n%3E360

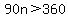
90n%3E360

n%3E4

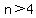So the smallest integer greater than 4 is 5.

Edwin