Find 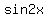 if
if  and
and 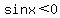
Since the secant and the sine of x are both negative, that means
x is in the third quadrant. between 180° and 270° in degress,
or between  and
and  in radians. So therefore
2x will be between 360° and 540° which is actually the 1st and
2nd quadrants. The sine is positive in both the 1st and 2nd
quadrants, so the answer will be posotive.
We need these identities:
1.
in radians. So therefore
2x will be between 360° and 540° which is actually the 1st and
2nd quadrants. The sine is positive in both the 1st and 2nd
quadrants, so the answer will be posotive.
We need these identities:
1.  2.
2.  3.
3.  First we'll find
First we'll find 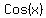 using 3.
using 3.
 Next we'll find
Next we'll find 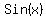 using 2.
using 2.






 However, since
However, since 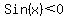 we take the negative sign,
we take the negative sign,
 Now we can substitute in 1:
Now we can substitute in 1:



 Edwin
Edwin